Les modeleurs déclaratifs

Née en 1989 ([LMM89]), la modélisation déclarative a donné naissance à de nombreux travaux. Nous allons nous attacher à effectuer un état de l’art, une synthèse, des principales connaissances et des principaux algorithmes existant sur ce sujet.

D’abord, nous présenterons les modeleurs déclaratifs et leurs différences avec les modeleurs traditionnels (section 2). Ensuite, nous présenterons les phases essentielles des la modélisation déclarative (section 3). Nous terminerons par une présentation des chapitres de cette première partie (section 4).

2. Modélisation classique et modélisation déclarative

Encore actuellement, avec un modeleur traditionnel, la création d’une scène se déroule en deux étapes :

· conception, calculs et vérification à la charge de l’opérateur ;

· visualisation à la charge du système.

L’utilisateur du modeleur doit, à partir de son idée, produire des spécifications puis, à l’aide de l’objet mental, les instructions élémentaires permises par le modeleur et nécessaires à la conception de l’objet. Le modeleur permet de visualiser l’objet mental ainsi décrit. Ensuite, une batterie de tests permettent de valider cette construction. S’ils sont négatifs, l’utilisateur doit revoir son objet mental et modifier les instruction entrées. Le processus recommence jusqu’à obtention d’une solution satisfaisante. Ensuite, si elle n’est toujours pas satisfaisante, il doit revoir ses spécifications.

«L’objectif de la modélisation déclarative de formes est de permettre d’engendrer des formes (ou des ensembles de formes) par la simple donnée d’un ensemble de propriétés ou de caractéristiques. L’ordinateur est chargé d’explorer l’univers des formes potentielles, afin de sélectionner celles correspondant à la définition donnée. Le concepteur n’a plus qu’à choisir, à l’aide d’outils appropriés, la ou les formes qui lui conviennent» [Luc93]. Aucune phase de tests n’est nécessaire puisque le modeleur produit des solutions en adéquation avec la demande de l’utilisateur. S’il ne trouve pas de solutions qui lui conviennent, il n’a alors qu’à modifier les propriétés fournies et à relancer une exploration. Ainsi, l’opérateur se trouve libéré des calculs et peut se focaliser sur la phase de création.

La Figure 1 illustre cette différence entre les deux types de modeleur. Les zones claires correspondent au travail effectué par l’homme et les zones foncées à celui réalisé par la machine. Les traits pointillés ‘.......’ mettent en valeur la correspondance des phases entre les deux types de modeleur. La position des boîtes indique qui de l’homme ou de la machine réalise l’action représentée ou la part respective de chacun. Une différence importante entre les deux approches est la quantité et le type de travail réalisés par l’homme. Les modeleurs déclaratifs assurent une part de travail beaucoup plus importante que les modeleurs traditionnels, laissant l’homme se concentrer sur les tâches de haut niveau. ([CDMM97])

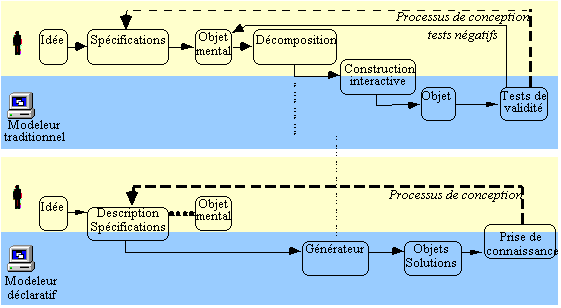
Figure 1. Comparaison de modeleurs traditionnel et déclaratif [CDMM97]

3. Les phases importantes d’un modeleur déclaratif

Il est possible de définir trois grandes phases dans l’utilisation d’un modeleur déclaratif ([LMM89], [Luc93] et [CDMM97] ; Figure 2) :

· la description de la scène qui permet de décrire ce que l’on veut obtenir ;

· le calcul des solutions ;

· la prise de connaissance des solutions obtenues.

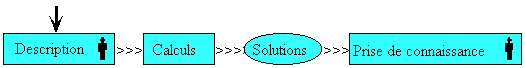
Figure 2. Vue globale d’un modeleur déclaratif [CDMM97]

Sur la Figure 2, la Figure 4 et la Figure 7 nous utilisons la même notation. Les actions sont représentées par des rectangles (voir Figure 3) et les informations par des ellipses. Une action peut être constituée de sous-tâches et de données. Une flèche sur un rectangle indique l’action qui est exécutée en premier. Les actions accessibles directement par l’utilisateur, c’est-à-dire celles avec lesquelles il interagit, sont marquées à l’aide d’un petit humanoïde (‘‘). Un losange traduit une condition. Enfin, les flèches constitués de chevrons (‘>’) soulignent un échange orienté de données entre 2 actions. Elles ne signifient en aucun cas une quelconque notion de séquencement.

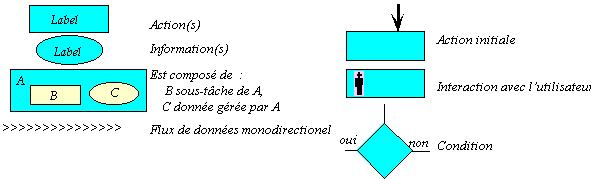
Figure 3. Notation des figures [CDMM97]

Remarque : Nous allons étudier, pour chacune de ses phases, les différents résultats qui ont été obtenus lors des différents DEA, thèses et conférences qui se sont déroulés principalement dans l’équipe MGII (certains travaux extérieurs à l’équipe ont été aussi étudiés : [Bel94], [BoP94], [ChC94], [Dje91], [Don93], [LiH94], [Mac92], [Ple94], [Tam95]…).

4. Organisation

L’organisation de cette partie suit les trois phases principales d’un modeleur déclaratif.

Nous présenterons d’abord la phase de description (chapitre 2). Nous y présenterons des idées de classement du vocabulaire utilisé. Nous étudierons les modes de saisies, la représentation et la structure d’une description.

Ensuite, nous nous intéresserons à la phase de calcul (chapitre 3). Nous ferons le tour des différents grandes méthode de génération qui ont été développées.

Puis, nous étudierons les outils de prise de connaissance de ces solutions (chapitre 4), c’est-à-dire quand, quoi et comment visualiser.

Enfin, nous terminerons par un panorama des techniques d’apprentissage développées pour la modélisation déclarative (chapitre 5).

Chapitre I.2
La phase de description

Les mots diversement rangés font un divers sens et les sens diversement rangés font différents effets.

Blaise PASCAL, Pensées, I-23

1. Introduction

La modélisation déclarative «repose sur l’idée que nous pouvons appréhender le “monde” autrement que par sa description géométrique : nous pouvons le percevoir par ses propriétés, par ses caractéristiques, c’est-à-dire non pas seulement par l’apparence qu’il nous présente mais par les mécanismes et les contraintes qui font qu’il nous apparaît sous cette forme. Ainsi, nous nous plaçons à un plus haut niveau d’abstraction» [LeG90].

La phase de description permet la gestion de la description de l’utilisateur. A l’aide des outils les plus adaptés au domaine d’application, il entre, d’une façon assez naturelle, les diverses propriétés qui constituerons la description de la scène qu’il désire obtenir. Les outils de description permettent aussi de modifier ou, éventuellement, de supprimer des propriétés. A ce niveau, le système effectue une vérification de la description afin de détecter contradictions, incohérence ou ambiguïté. Parfois, lorsque c’est nécessaire, le modeleur demande à l’utilisateur des précision afin de tenter de résoudre ces problèmes. La description est finalement envoyée au module d’exploration (de calcul) afin qu’il génère les solutions (Figure 4).

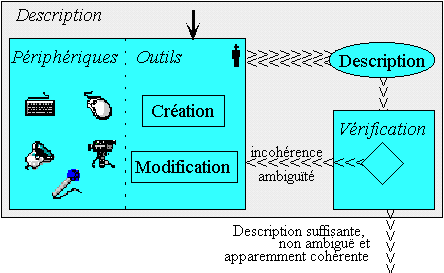
Figure 4. La phase de description [CDMM97]

Remarque : La description qu’il fournie n’est pas forcément totalement cohérente, car certains cas ne peuvent être détecter que lors de la génération.

Dans un premier temps, à travers l’étude du vocabulaire utilisé (dans le cas d’une description textuelle), nous nous intéresserons aux caractéristiques décrites dans la description (section 2). Nous verrons que, malgré une forte dépendance au domaine d’application, il tout de même possible de mettre en évidence des traits généraux. Nous étudierons ensuite les caractéristiques de la description (section 3). Nous parcourrons ensuite les différents modes de description utilisé (section 4). Puis nous détaillerons les différents modèles de description et de structure de scène (modèle interne de la description) qui ont été proposés. Enfin, nous exposerons les différentes remarques effectuées autour des problème de gestion de la cohérence.

2. Le vocabulaire

2.1. Introduction

Pour que l’utilisateur puisse décrire facilement et naturellement la scène ou l’univers qu’il désire créer, il est indispensable de lui fournir un vocabulaire adapté et performant. Celui-ci doit lui permettre d’énumérer les différentes propriétés et caractéristiques qu’il veut imposer. Cette énumération s’appelle une description. Elle peut être précise ou imprécise, détaillée (accès aux informations standard telles que les coordonnées) ou approximative (description intuitive, sans coordonnées, en oubliant certaines caractéristiques), globale ou locale, particulière ou générale. Cette description permet la constitution d’un ensemble de propriétés. A partir de ce dernier, l’exploration des formes de l’univers permet d’extraire celles répondant à la description. Elles seront appelées formes solutions.

A priori, le vocabulaire semble fortement dépendant de l’application utilisée. Cependant, un certain nombre de points communs, de lignes générales se retrouvent dans toutes les applications. En particulier, la modélisation déclarative en synthèse d’image nécessite toujours un vocabulaire lié à l’image et à la notion de représentation visuelle.

Le problème du vocabulaire a toujours été présent dans les différents projets mais il ne fait réellement l’objet d’une étude précise que depuis peu de temps (sauf pour [Bea89], les applications traitant explicitement du vocabulaire sont récentes : [MaM89-94], [Chau92], [Chau94], [Paj94a-b], [Pou94a], [Mou94], [Dem94], [Dan95], [Fau95], [DaL96], [Lie96] et [Luc97]). Nous étudierons les grands traits du vocabulaire lié à un domaine d’application et nous tracerons les traits généraux du vocabulaire que l’on retrouve dans une majorité d’applications.

2.2. Le vocabulaire dépendant du domaine d’application

Chaque application possède un vocabulaire bien particulier. D’une part, il est technique, spécifique au domaine traité et aux propriétés utilisées (cf. le vocabulaire utilisé par [MaM91], [Paj94b], [LuP94]...). D’autre part, toutes les descriptions faisant référence à des propriétés de nature fonctionnelle sont caractéristiques du domaine d’application.

Certains termes utilisés pour décrire des effets visuels spécifiques au domaine sont aussi souvent présents. Par exemple, on trouve la notion de “guirlandes” dans [Mar90] ou les termes de “fraisage” dans [Ker89]... Ces termes peuvent représenter des phénomènes plus généraux mais sont bien spécifiques à l’application.

En général, le vocabulaire spécifique dépend, entre autres, des éléments de base utilisés, de leurs caractéristiques, des paramètres les définissant et de leur utilisation dans la forme à générer. Les modes de construction (les opérations élémentaires de construction) sont aussi très importants dans le vocabulaire.

La catégorie d’utilisateur qui va travailler sur l’application est aussi un facteur important dans la définition de l’ensemble du vocabulaire. Les termes utilisés ne seront pas les mêmes selon qu’il s’agit d’un utilisateur quelconque ou d’un spécialiste dans le domaine. Il serait même intéressant que les applications puissent fonctionner selon deux modes différents : le mode utilisateur standard et le mode expert.

On trouve aussi une autre catégorie de vocabulaire : celui défini par l’utilisateur. Dans certaines applications (par exemple [Chau94]) l’utilisateur peut créer son propre vocabulaire. Les nouveaux termes sont, actuellement, des combinaisons (conjonctions, disjonctions, négations...) de termes existants ou déjà définis, des synonymes ou des antonymes. Mais rien n’empêche, dans un proche avenir, de définir de nouveaux termes en donnant leur définition à l’aide de règles d’inférences ou de procédures de calcul.

Afin de bien déterminer le vocabulaire spécifique, le concepteur du système doit faire une étude bibliographique des termes utilisés dans le domaine. Il serait intéressant qu’il soit aidé dans cette tâche par un outil logiciel comme ANA (“ANA (Apprentissage Naturel Automatique) est un système de détermination automatique de terminologie pour la construction du thesaurus d’un domaine.” [Eng93]) permettant de récupérer sur un corpus spécifique au domaine les termes les plus fréquemment utilisés.

Néanmoins, il existe du vocabulaire suffisamment général pour être présent dans une grande partie des applications.

2.3. Le vocabulaire général

D’abord, faisons un constat : nous sommes en synthèse d’image. Et qui dit « image » dit « représentation graphique » et « effets visuels ». A partir de cette remarque, nous pouvons donc déduire qu’il doit y avoir, malgré tout, certains points communs dans les vocabulaires des différentes applications. Une partie de ce vocabulaire est générale à toute application de CAO tandis qu’une autre est plus particulière aux systèmes déclaratifs. Nous allons donc regarder les différentes règles que l’on peut tirer de ce vocabulaire général. Puis nous étudierons les différentes catégories de vocabulaires (le plus étudié dans la littérature est le vocabulaire concernant les dimensions, le placement et le positionnement).

Les méthodes de description ont pour objet la manipulation d’un vocabulaire (porteur de concepts) permettant de décrire les propriétés de la forme désirée. Une des difficultés essentielles va être de définir un vocabulaire adapté, précis, suffisamment riche pour permettre une certaine souplesse et décrire un maximum de choses, et, minimal pour limiter les redondances et les ambiguïtés.

[MaM89-94], [Bea89], [Chau92], [Don93], [Pou94a], [Paj94a-b], [Mou94], [Dem94], [Dan95] et [Fau95] ont ainsi essayé de définir et d’étudier le vocabulaire utile à la description d’une scène.

[Bea89] propose de classer ce vocabulaire en classes de descripteurs. Il en propose huit :

1. Les descripteurs de formes. Ils comprennent l’ensemble des propriétés de forme tant au niveau global que local.

2. Les descripteurs géométriques. Ils ne caractérisent pas l’objet lui-même mais les relations et les positions des formes associées à l’objet. Ils donnent les correspondances de position, forme, mesure...

3. Les descripteurs topologiques. Ils déterminent les propriétés qui sont préservées par des déformations continues.

4. Les descripteurs de relations spatiales. Ils permettent de localiser dans la forme les zones où une primitive de forme intervient et de placer les différentes primitives de forme les unes par rapport aux autres.

5. Les descripteurs de décomposition. Ils distinguent différentes parties au niveau de la forme (pas forcément en constituants élémentaires). Ils permettent de simplifier la description. Il est possible, par exemple, d’associer à chaque partie une zone d’expansion (zone de l’espace).

6. Les descripteurs de fonction. Ils décrivent le rôle joué par l’entité dans son environnement.

7. Les descripteurs d’héritage. Ils expriment le fait qu’un objet possède les mêmes propriétés qu’un objet plus général. Ils mettent en place une arborescence qui va du plus général au plus spécifique. Ils introduisent la notion de style.

8. Les descripteurs de relations inter-objets. Ils permettent la description des relations existant entre deux objets ou entre un objet et son environnement.

Remarque : certains descripteurs sont évalués d’une manière algorithmique (un programme décide si une forme répond ou non à la description) et d’autres par un calcul déterminé (une valeur est associée à la forme pour une description donnée). Cette dernière catégorie va être gérée par ce que nous appellerons les propriétés mesurables. [Pou94b] souligne qu’il est préférable (quand c’est possible), pour une meilleure compréhension de la forme, de calculer des pourcentages plutôt que des valeurs brutes. En effet, un pourcentage possède la faculté de se suffire à lui-même alors qu’une valeur brute demande des connaissances supplémentaires sur la forme.

[Bea89] introduit aussi la notion de multi-description (notion reprise dans [Ple91]). Cela permet de prendre en compte plusieurs pour un objet donné propriétés. Nous verrons qu’au vocabulaire (aux descripteurs) nous allons faire correspondre des propriétés. Les deux notions étant très liées, elles seront utilisées indifféremment. Ces propriétés peuvent être contradictoires. Il est nécessaire de leur attribuer une importance plus ou moins grande. Les formes obtenues seront alors des compromis entre ces propriétés. Chaque propriété est évaluée par rapport à la propriété idéale (pourcentage de vérification).

[Chau92] montre qu’il est important de bien choisir son vocabulaire. Elle propose d’utiliser des mots usuels pour appréhender le maximum de situations. Cependant, le concepteur doit faire attention d’une part à ne pas surcharger la liste des mots par des redondances et, d’autre part, d’en choisir suffisamment afin de rendre compte de la richesse des situations. Elle souligne aussi un problème délicat : éviter autant que possible les mots possédant une certaine ambiguïté. Pour cela, les mots doivent être choisis en fonction de leurs définitions littéraires (dictionnaires courants), scientifiques et usuelles.

Comme le souligne [Fau95], il faut faire attention à l’idéalisation des entités décrites (l’idéalisation d’une entité est l’ensemble des propriétés auxquelles nous attachons une importance particulière). Il faut bien étudier le vocabulaire afin de déterminer toutes les propriétés, explicites et implicites, associées à un terme. De plus, il faut se méfier du “bon sens” pour la sémantique des mots. Cette notion n’est pas si simple car elle dépend de critères culturels.

Les travaux de [Paj94a-b], [Pou94a] et [Chau92-94] (entre autres) mettent en évidence trois classes de vocabulaire dans une application “déclarative” :

· Le vocabulaire de description. Ce vocabulaire permet d’énumérer les différentes propriétés que devront respecter les formes solutions. Il correspond aux descripteurs que nous venons de citer.

· Le vocabulaire de modification. Il donne la possibilité de modifier une forme solution sans avoir vraiment à la générer à nouveau entièrement. Il va permettre d’indiquer des modifications locales et relatives sur certaines parties de la forme (déplacement...). Il sera particulièrement utile pour les méthodes que nous appellerons les méthodes de génération par échantillonnage.

· Le vocabulaire “opératoire”. Il sera utile pour expliquer les formes obtenues et, après l’obtention d’une forme solution intéressante, afin que le système puisse décrire clairement le mode opératoire permettant de “construire” l’objet correspondant.

Globalement, nous constatons que le vocabulaire de description peut être décomposé en cinq sous-classes :

· Les caractéristiques visuelles (ou caractéristiques graphiques). Elles concernent les termes portant sur : la couleur, les textures, la visualisation et la position de l’observateur et des sources lumineuses.

· La description d’un objet. Cela correspond aux termes portant sur : la géométrie et la topologie, la forme générale, les dimensions, le placement et le positionnement (avec en particulier les études de [Van86]) ainsi que les comparaisons entre objets.

· La “manipulation” d’objets. Les termes portent sur : l’organisation de la scène et les variations, l’énumération et la désignation.

· Les quantificateurs. Ils caractérisent et modifient les différentes descriptions d’une manière plus ou moins précise. + imprécision

· La combinaison de descriptions. Les termes de cette sous-classe permettent de fournir une description riche en donnant plusieurs caractéristiques à un objet.

Le vocabulaire de description se répartit en deux catégories :

· Le vocabulaire absolu. Les propriétés sont décrites indépendamment du reste de la scène. Parfois, est considéré comme absolu le vocabulaire relatif par rapport à l’univers car il ne fait pas référence à un autre objet.

· Le vocabulaire relatif. Il fait référence à des propriétés données en fonction d’objets déjà existants. Souvent, l’interprétation de ce vocabulaire pose des problèmes.

D’après [Chau92-94], une description est une liste de propriétés (définies par un vocabulaire donné), absolues ou relatives, éventuellement précédées d’une ou plusieurs modifications ou par une négation, séparées par des connecteurs “et” et “ou”. [Chau92] en déduit deux types de description :

· les descriptions absolues où toutes les propriétés sont absolues (utilisation uniquement d’un vocabulaire absolu) ;

· les descriptions relatives où la liste des propriétés comporte au moins une propriété relative.

Nous ne rentrerons pas ici dans le détail du vocabulaire utilisé en modélisation déclarative. Pour cela, on peut se reporter à [Des95a], [LuD96] et [Luc97].

Remarques :

· Il faut faire attention aux termes apparemment univoques. Prenons par exemple le terme “symétrique”. Sans parler des différents types de symétries qui existent (centrale, axiale et planaire), plusieurs interprétations sont possibles suivant l’objectif de l’utilisateur : “géométriquement symétrique” (sens mathématique), “visuellement symétrique”, “physiquement symétrique”... Il est important de bien définir les termes autorisés afin de lever le maximum d’ambiguïtés.

· Le vocabulaire utilisé et la sémantique qui en résulte ne sont pas toujours évidents à manipuler. Par exemple, comment représenter des dimensions infinies ? Ce problème est souligné par [Fau95] pour l’étude de la description d’un plan. Il propose de choisir, de préférence, une représentation mettant en jeu des références culturelles et prenant en compte les limitations de la perception visuelle (limitations et cadre naturel).

· Il est important de noter que, tant pour les dimensions que pour d’autres propriétés comme le placement et de positionnement, les notions sont totalement subjectives. Dans le cas où l’univers se rapporte à une boîte englobante finie, les notions de grandeur peuvent être rapportées à un pourcentage de la taille de l’univers. Mais, dans le cas où l’univers est infini, ces notions deviennent difficiles à calculer. En fait, elles dépendent des autres objets et de la distance de l’utilisateur par rapport à la scène. Dans ce cas, la notion de grandeur, par exemple, peut servir à fixer une distance convenable entre l’utilisateur et la scène lors de la visualisation. Ceci apporte donc des informations pour la recherche d’un bon point de vue (voir le chapitre sur la prise de connaissance des solutions). Ces problèmes sont aussi soulignés par [Fau95]. Il montre que l’observation dépend de l’environnement d’observation et des notions de “moyennes” implicites. Pour lui, une description devrait être composée d’un ensemble de couples (propriété, espace de référence associé). Cet espace est, si possible, implicite. Cela permet d’avoir un vocabulaire fini et plus facile à manipuler. Cependant, la notion d’espace de référence est complexe et demande à être étudiée plus profondément.

3. La description

La description de la scène est modélisée (codée) à l’aide d’un ensemble de propriétés. Cet ensemble détermine le modèle abstrait ou modèle déclaratif de la forme.

A l’ensemble des descripteurs, on associe un ensemble de propriétés. Les formes qui respectent ces propriétés (description) sont appelées formes solutions (objets solutions). Comme les descripteurs, les propriétés sont de différentes natures : topologiques, géométriques, mécaniques...

Elles ont différentes caractéristiques :

· générales c’est-à-dire indépendantes de l’application, ou spécifiques à l’application,

· objectives (calculables précisément), ou subjectives (impressions...),

· globales (sur toute la forme), ou locales (sur une partie de la forme).

La description correspond à une combinaison de conjonctions et/ou de disjonctions de propriétés. Celles-ci peuvent être composées (union, intersection, négation... de propriétés élémentaires). Elles peuvent être mises en relation à travers des notions telles que celles de sur-propriété ou de sous-propriété (voir plus loin).

Ces descriptions (et donc ces propriétés) seront transformées en modèle interne. Le modèle interne dépendra du générateur envisagé :

· pour les arbres de construction, une base de faits et de règles ;

· pour les arbres d’exploration, un modèle spécifique ;

· pour les systèmes à contraintes, des tables sémantiques.

Il est parfois utile de définir des valeurs par défaut pour certaines propriétés afin de pouvoir générer des solutions quelle que soit la description (cf. règles de suppléance dans [MaM90]).

Remarque : Le modèle interne lié aux propriétés de la description est important. Il permet de rendre compte de la sémantique de ces propriétés. Les différents modèles classiques sont présentés au chapitre II.1 en introduction au formalisme que nous proposons (Partie II).

4. Modes de description

4.1. Introduction

La description peut se faire selon trois modes différents :

1. les menus et fenêtres de dialogue ;

2. les phrases en langage naturel ;

3. les descriptions graphiques.

Ces modes ne sont pas exclusifs. Ils peuvent être combinés afin de rendre plus puissante et variée cette description (Figure 5). [Ple91] souligne qu’une interface de modeleur déclaratif doit être claire et souple.

Figure 5. Description textuelle + schéma Þ scène possible

Voici quelques exemples :

· [Mar90b] combine la description graphique et les menus pour décrire les automates (projet AutoFormes). Ce projet consiste à définir, de manière déclarative, des motifs d’automates cellulaires. A partir de la description, le système recherche les fonctions de transition qui vérifient les propriétés.

· [Char87], [Ker89] et [Pou94b] font de même pour décrire les triplombres (projet SpatioFormes - [Pou93], [Pou94a], [Pou94b] et [Pou96]). Ce projet à pour but d’étudier les techniques de description et de génération de matrices d’énumération spatiales (matrices de voxels). La description peut se faire à l’aide de triplombres.

· [Chau92-94ab] mélange les trois modes pour décrire les boîtes, les graphes de proximité et les techniques de croissance (projet VoluFormes). Ce projet consiste à étudier les techniques de résolution de descriptions à l’aide de système de contraintes. Il permet la description de scènes sous contrôle spatial. Il étudie aussi les techniques de croissance sous contrôle spatial.

· [LuP94] utilise aussi bien les menus et les boîtes de dialogue que les outils graphiques et les descriptions à l’aide de phrases (projet MégaFormes - [LuP94] , [Blo96] et [PoL96]]). Ce projet a pour objectif de générer des mégalithes à partir de leur description. C’est une application du projet SpatioFormes.

Remarque : Un triplombre est un ensemble de trois ombres portées (2D) sur trois plans orthogonaux (lumière considérée à l’infini). A un triplombre, on peut associer un nombre fini (ou nul) de matrices de voxels (3D).

4.2. Les menus

La technique de description la plus répandue est celle qui utilise des menus et des boîtes de dialogue. Les différentes caractéristiques sont présentées à l’aide de boîtes de dialogue adaptées. Les propriétés sont choisies à l’aide de cases à cocher, de “boutons radio” ou de menus déroulants spécifiques. Toutes les “valeurs” possibles des propriétés sont proposées.

L’utilisateur choisit les propriétés qui l’intéressent ainsi que leur “valeur”. Cette technique est utilisée dans toutes les applications du projet ExploFormes ([LMM89], [Luc97] ; englobe tous les projets cités : AutoFormes, PolyFormes, PastoFormes, SpatioFormes, FiloFormes, MégaFormes, VoluFormes, CurviFormes, MultiFormes...) : [Col90b] (projet PastoFormes qui étudie la description d’objets obtenus par collages de polyèdres élémentaires - [Col87], [Col88], [Col90a], [Col90b], [Col91] et [Col92]), [Mar90b], [MaM89-92] (projet PolyFormes qui consiste à générer tous les polyèdres réguliers ou semi-réguliers répondant à certaines propriétés), [Chau92-94], [Char87], [Ker89]... Elle utilise toutes les possibilités proposées par les techniques d’interface afin de rendre la description plus facile, rapide et confortable. L’espace de visualisation est alors dégagé la plupart du temps pour visualiser en permanence la scène (Voir [Chau92]). Les erreurs de syntaxe sont ainsi évitées.

Les propriétés sont déterminées à l’aide d’un vocabulaire bien particulier. Il permet à l’utilisateur de faire facilement une description claire et précise. Ce vocabulaire, nous l’avons déjà vu, a commencé à être étudié par [MaM89-92], [Pou94a], [Paj94a] (projet FiloFormes qui consiste à étudier la génération de segments de droites dans un plan et qui est appliqué par le logiciel FiloTableaux qui génère des tableaux de fils répondant à une description - [Paj94a], [Paj94b] et [Luc94]), [Chau92-94], et, [Dan95] (projet CurviFormes qui a pour objectif la génération de courbe et surface à l’aide de la modélisation déclarative - [Dem94], [Dan95], [Rob96], [DaL96a] et [DaL96b]).

4.3. Le langage naturel

Une autre possibilité est de permettre une description de l’univers à l’aide de phrases en langage naturel. La description est alors plus souple et ne demande pas une grande maîtrise de l’interface.

L’utilisateur décrit verbalement la scène qu’il veut voir par différents moyens :

· par l’intermédiaire du clavier,

· par écrit (à l’aide d’un scanner par exemple),

· par oral en utilisant un microphone.

Dans certains cas, il existe des descriptions de formes dans des textes ou des enregistrements. Il n’est pas toujours possible de traduire facilement et rapidement ces descriptions par une série de commandes sur des menus ou par un schéma. Il est donc intéressant de pouvoir utiliser la description telle quelle c’est-à-dire d’analyser et d’interpréter les phrases en langage naturel.

Le besoin de pouvoir générer des formes correspondant à une description écrite est nettement mis en évidence dans [LuP94]. En effet, il existe de nombreuses descriptions écrites de mégalithes qu’il serait intéressant de pouvoir directement utiliser.

Le projet MultiFormes, qui étudie la génération de scènes par des descriptions complexes et structurées ([Bea89] et [Ple91]), essaie de trouver le vocabulaire à utiliser pour décrire une scène et la générer.

[Chau92-94] donne aussi la possibilité de construire une phrase à l’aide d’un vocabulaire spécifique (voir l’apprentissage).

[Dje91] propose la mise en place d’un interpréteur de description comportant analyseur lexical, syntaxique et sémantique. Cependant, là encore, la grammaire mise en place (non contextuelle) demande encore une syntaxe de la description très rigoureuse.

Dans les trois cas, nous pouvons plutôt parler de langage “quasi-naturel”. En effet, ils ne prétendent pas recréer des programmes d’analyse de phrases en langage naturel, ce problème étant suffisamment difficile. Ils utilisent des grammaires et des analyseurs très contraignants ainsi qu’un vocabulaire rigide et limité.

Remarque : dans certains projet (en particulier avec [Gra96]) le langage utilisé est très formel. Ils utilisent des combinaisons d’opérateurs sur des ensembles ou des variables. Ainsi l’analyse et la modélisation en sont extrêmement facilités.

Cela nous amène à mettre en évidence un des problèmes essentiels de ce genre de technique : il faut apprendre la syntaxe et le vocabulaire propres à l’application. La description qui en découle risque donc d’être dans un langage qui ne soit pas facile à utiliser.

4.4. Les descriptions graphiques

Les techniques de description à l’aide de vocabulaire ne sont pas toujours idéales. Il est souvent nécessaire d’en utiliser d’autres comme, principalement, les descriptions graphiques.

Parfois, il est en effet plus facile de décrire avec un dessin, une image ou un schéma certaines propriétés que devront respecter les formes de l’univers. Cela permet de décrire certaines caractéristiques d’une manière plus intuitive. Un dessin permet de mettre en place des notions qui sont difficiles, voire impossibles, à décrire par un vocabulaire suffisamment précis et concis. Cela permet aussi une description plus condensée.

[Mar90b] (AutoFormes) utilise cette technique pour donner la possibilité à l’utilisateur de décrire un motif qu’il aimerait voir dans les images engendrées par un automate.

[Char87], [Ker89] et [Pou94a] (SpatioFormes) utilisent le dessin comme base de la description. Ils créent des objets (triplombres) à l’aide de trois ombres.

[Chau94] utilise un schéma afin de mettre en place le graphe de proximité des volumes. Ici, le schéma n’influence plus directement l’image de la scène. Il n’apporte pas des propriétés sur caractéristiques visuelles mais sur la méthode de génération.

4.5. Conclusion

Actuellement, la gestion de ces modes n’est que très peu étudiée. Les applications utilisent encore en majorité les menus ou la description textuelle. Les modes de description sont un aspect important des modeleurs déclaratifs. Les systèmes déclaratifs doivent y attacher de l’importance. A l’avenir, il sera important d’étudier plus précisément l’utilisation d’autres techniques ainsi que la gestion de plusieurs modes utilisés simultanément (par exemple : vidéo et paroles).

Remarque : [GCR93] énumère, avec le projet MODEMM, toutes les techniques intéressantes pour un tel système : reconnaissance de la parole, synthèse vocale, clavier, graphique, analyse d’images (module de vision), système de réalité virtuelle (gants de données et casque de visualisation stéréoscopique)... De telles interfaces sont appelées interfaces multimodales.

5. Structuration d’une description

Nous venons de recenser les divers éléments que l’on trouve dans un modeleur déclaratif. Nous allons étudier maintenant comment ils sont structurés entre eux.

Remarque : leur gestion et leur interprétation n’est pas abordée dans ce chapitre mais seulement dans la suivante.

5.1. Structure d’une scène

[MaM94] et, surtout, [Ple91] mettent en évidence l’intérêt de structurer la description dans le cas de scènes ou de formes très compliquées. Cela permet d’enrichir la description, d’améliorer la connaissance de la scène, la génération et la visualisation. Nous avons déjà vu un certain nombre de termes permettant d’organiser une description.

En s’inspirant des différents niveaux d’abstraction de l’espace architectural présenté par [Mac92] et [Don93], nous pouvons classer les entités manipulées en modélisation déclarative en cinq niveaux d’abstraction :

1. le constituant ou objet élémentaire défini par une liste de paramètres (par exemple un voxel, un segment, un cellulon, etc.) ;

2. l’objet simple composé d’objets élémentaires et décrit par une liste de propriétés portant sur tout l’objet (par exemple la matrice de voxels connexes, un ensemble de collage de polyèdres, un rocher, etc.) ;

3. l’objet complexe composé d’un ensemble connexe d’objets simples ou complexes (par exemple une théière, une maison, etc.) ;

4. le groupe composé d’un ensemble d’objets complexes (par exemple un quartier, etc.) ;

5. la scène composée d’un ensemble de groupes (par exemple un paysage, etc.).

Une scène constituée uniquement des niveaux 0 et 1 est appelée scène simple. Autrement dit, une scène simple est une scène dont les propriétés peuvent être décrites de façon simple, c’est-à-dire à l’aide d’un nombre réduit de termes.

Une scène constituée de niveaux supérieurs à 1 est appelée scène complexe. C’est une scène dont l’ensemble des propriétés caractéristiques ne peut pas être décrit de façon simple. Par conséquent, ces scènes sont difficiles à décrire. Il faut un effort de décomposition spatiale et logique afin de rendre plus aisée la description de chaque partie. Une partie est alors soit une scène simple soit une composition de sous-scènes (scène complexe).

[Ple91] propose deux méthodes de description pour la construction de scènes complexes :

· la décomposition hiérarchique,

· la composition.

5.2. Décomposition hiérarchique

La description par décomposition hiérarchique est une description résultant d’une analyse descendante de la scène (du plus général au plus précis). Elle est représentée par un arbre n-aire de profondeur quelconque. A chaque niveau on fait correspondre un niveau de détail. Plus on descend dans l’arbre, plus la description est précise. Cela permet, pour chaque composante de la scène, une description à un niveau de détail quelconque choisi librement par l’utilisateur. Les feuilles de l’arbre sont considérées comme des scènes simples.

A chaque nœud de l’arbre, sont associées une description :

· des propriétés de haut niveau souhaitées (forme...),

· des contraintes de taille,

· des contraintes spatiales entre les nœuds enfants lors de la décomposition d’un nœud,

· des contraintes de taille inter-objet.

Cette famille de description semble intéressante quand la forme (la scène) est composée de plusieurs “sous-formes” plus ou moins indépendantes. Elle permet de gérer convenablement les propriétés de forme et de placement.

Il existe deux types de décomposition hiérarchique :

1. la décomposition spatiale ;

2. la décomposition fonctionnelle.

5.2.1 Décomposition spatiale

La scène est décomposée en sous-scènes dont les boîtes englobantes sont disjointes. Seulement, avec ce type de décomposition, certains objets sont difficiles à décrire. De plus, cette démarche n’est pas toujours naturelle : il est parfois difficile de décrire le contenu de chaque boîte. Par contre, elle permet un contrôle efficace du parcours des arbres de génération.

5.2.2 Décomposition fonctionnelle

La scène est décomposée en parties fonctionnelles. Le découpage est effectué en tenant compte des fonctions de chaque partie de la scène. Cette décomposition est plus intuitive. Elle implique une division de l’espace en boîtes englobantes autorisant les recouvrements.

Pour la description des différentes parties, trois possibilités de description se présentent :

1. explicite (la scène est décrite explicitement, éventuellement par décomposition) ;

2. implicite (la description existe par ailleurs) ;

3. approximative (à l’aide de quelques propriétés simples).

5.2.3 Difficultés de description

La description d’une scène (ou d’une partie de scène) bien connue intuitivement pose parfois certains problèmes. Plusieurs solutions de description sont alors possibles :

· par décomposition supplémentaire (décomposition forcée et pas toujours naturelle) ;

· procédurale (description impérative intégrée à la description sous forme de coordonnées de points...) ;

· par apprentissage (description initiale grossière puis affinée par apprentissage jusqu’à obtenir une situation proche de celle souhaitée) ;

· par composition (intégrée ensuite dans l’arbre de décomposition hiérarchique).

Remarque : pour la description par apprentissage, [Ple91] propose : soit un parcours systématique d’un espace de solution soit l’utilisation d’un croquis par exemple. En fait, les deux solutions proposées sont plutôt proches des techniques de modélisation déclarative. La scène posant des problèmes est alors considérée comme une scène à générer et est traitée à part.

5.3. Composition

La description par composition est une description résultant d’une analyse ascendante de la scène (regroupement d’objets de plus en plus complexes). Au départ, l’utilisateur dispose d’un ensemble extensible d’objets de base (formes générales, objets génériques, classes d’objets). Chaque nouvel objet est composé à partir des objets de base ou des objets précédemment créés. La dimension des objets peut changer en cours de construction.

La description est, là aussi, un arbre dont les feuilles sont des objets de base et à chaque nœud on a :

· un ensemble facultatif de propriétés de forme ;

· un ensemble facultatif de contraintes de taille ;

· un ensemble de contraintes spatiales sur les enfants ;

· un ensemble de contraintes de taille inter-nœuds.

Cette famille de description nécessite de bien connaître les objets de base et le résultat de leurs compositions. Cette composition peut être logique ou spatiale.

5.4. Arbre syntaxique et sémantique

Ces deux types d’organisation d’une description mènent à un arbre de description syntaxique, le plus souvent n-aire (n ≥ 2). Pour une description donnée, plusieurs arbres sont possibles s’il existe des alternatives aux différents niveaux. Bien sûr, lors de la génération, tous les arbres seront à explorer entièrement (sauf conditions particulières pour des élagages) pour trouver toutes les solutions possibles. L’arbre obtenu est de profondeur finie ou infinie (dans le cas d’une description récursive). Cependant, si l’arbre est infini, sa profondeur sera limitée artificiellement. A chaque nœud de l’arbre on considère la description d’une scène courante composée de propriétés et de sous-scènes (ses fils).

Pour chaque arbre syntaxique, il peut y avoir plusieurs arbres sémantiques. En effet, si une partie de la description est approximative, plusieurs valeurs de paramètres seront autorisées. Nous aurons alors autant d’arbres sémantiques que de valeurs possibles.

5.5. Propriétés locales et globales

Les propriétés du nœud courant peuvent être :

· locales, c’est-à-dire qu’elles ne concernent que le nœud courant (la scène courante) ;

· globales, c’est-à-dire qu’elles influent aussi sur les sous-scènes de la scène courante.

Pour [Ple91], les propriétés globales doivent, quand cela est possible, être transmises aux sous-scènes (nous appellerons cela l’héritage). Pour une scène donnée, il faut d’abord traiter les propriétés locales puis les propriétés globales (soit celles qui apparaissent à ce niveau, soit celles héritées de la scène “mère”). Ces dernières doivent être prioritaires par rapport aux propriétés locales. Elles doivent donc s’appliquer en dernier.

6. Problèmes de cohérence de la description

Le problème de cohérence de la description (vérification et traitement) se pose très souvent. Pour gérer une situation d’incohérence ou d’aberration, plusieurs comportements sont possibles (cf. [Chau92-94], [MaM90], [Bea89] et [Ker89]) :

· refuser la description ;

· proposer le problème à l’utilisateur afin qu’il décide lui-même ;

· expliquer le problème et demander une nouvelle définition ;

· proposer des solutions ;

· résoudre le problème d’office.

Plusieurs choix de traitement sont alors possibles :

· “oublier” la ou les propriétés en cause dans l’incohérence (notion de filtre) mais le problème est de définir combien et lesquelles ([Pou94b] propose d’éliminer de préférence les propriétés qui génèrent le plus de contradictions) ;

· trouver un compromis entre les propriétés contradictoires pour trouver des solutions intermédiaires quand c’est possible (notions de multi-description et de déformation présentées dans [Bea89] et [Ple91] et notions de propriétés “à peu près” satisfaites dans [Pou94b]) ;

· donner un classement en fonction des priorités associées aux propriétés.

Remarques :

· Selon [Bea89] la notion de déformation correspond à une succession d’opérations élémentaires permettant d’ajouter à la forme considérée une propriété donnée tout en préservant plus ou moins celles définies préalablement. Ces déformations sont, pour lui, au niveau géométrique.

· En cas de contradiction, le système essaye, si c’est possible, une vérification “à peu près” des propriétés. Pour cela, il est susceptible de modifier les propriétés afin de tendre vers ce compromis.

[Pou94b] montre aussi un autre cas de contradiction : la “concurrence” entre propriétés locales et propriétés globales. En effet, il arrive qu’une même propriété soit applicable à la fois au niveau local et au niveau global. Généralement, il est préférable de traiter d’abord les propriétés au niveau local (sur chaque objet de la scène) puis au niveau global (sur tous les objets de la scène). Le traitement d’une propriété à la fois demandée en local et en global est assez délicat. En effet, les deux descriptions ne sont pas forcément totalement cohérentes. [Pou94b] propose alors de traiter en priorité les propriétés locales. Puis, l’application de la propriété globale se fait à l’aide de légères modifications des objets de la scène. Ces modifications (sortes de “déformations” mais pas seulement géométriques) sont réalisées en essayant de changer le moins possible les propriétés locales (quitte à utiliser des subterfuges tels que la modification du fond de la scène).

Dans le cas d’un système à base de contraintes, nous verrons que [Chau92] propose différentes solutions pour traiter les contradictions, dont une proposition de gestion de compromis.

[Mou94] met en évidence un problème de cohérence au niveau de la modification d’une description. En effet, l’utilisateur ne doit pas proposer n’importe quelle modification. Cela dépend de la description de départ et des modifications précédentes.

Il souligne quatre problèmes principaux :

1. Le paramètre associé à la propriété augmente sans atteindre la valeur voulue. Il faut alors gérer la progression lorsqu’on arrive près de la limite.

2. La limite du paramètre (borne de l’intervalle de validité) est atteinte et l’utilisateur veut encore progresser. Il faut prévenir l’utilisateur que la limite est proche puis, s’il insiste, provoquer un message d’erreur.

3. La limite du modificateur (la fourchette dans l’intervalle de validité) est atteinte et l’utilisateur veut encore progresser. Il faut prévenir l’utilisateur que la limite est proche puis, s’il insiste, lui proposer une nouvelle modification, le modificateur étant mal choisi.

4. Les différentes modifications successives d’un paramètre ne sont pas cohérentes. L’utilisateur doit alors revoir sa description et reprendre les modifications.

7. Forme “belle”

Nous avons vu, que le vocabulaire utilisé est parfois (souvent) subjectif. Il a été émis le désir ([Dem94]) de pouvoir utiliser certains termes tels que : “Beau”, “Esthétique”, “Parfait”, “Élégant”... Il semble que ceci est difficilement utilisable (voir impossible à gérer). En effet, comment déterminer que quelque chose est “beau” ?

La notion de beauté dépend de beaucoup de “paramètres” :

· du concepteur, de son expérience, de son caractère, de son humeur du moment, de ses origines culturelles (Voir [Hall66])... ;

· de l’application dans le cas où “beau” signifie “techniquement bien fait” (les critères de beauté sont alors plutôt des critères techniques) ;

· de ce que veut faire le concepteur dans le cadre de la manipulation courante.

«...les principes du plaisir ne sont pas fermes et stables. Ils sont divers en tous les hommes, et variables dans chaque particulier avec une telle diversité, qu’il n’y a point d’homme plus différent d’un autre que de soi-même dans les divers temps. Un homme a d’autres plaisirs qu’une femme ; un riche et un pauvre en ont de différents ; un prince, un homme de guerre, un marchand, un bourgeois, un paysan, les vieux, les jeunes, les sains, les malades, tous varient ; les moindres accidents les changent.» [PASCAL, Pensées, I-3]

Pour toutes ces raisons, il n’est pas possible de mettre en place des concepts tels que la “beauté” et les concepts d’esthétisme en général. Une forme “Belle” n’est-elle pas, en fin de compte, une solution choisie par l’utilisateur ? La description “Belle” n’est-elle pas, en réalité, le résumé de toutes les propriétés de la description et celles qu’il a oublié de mentionner ?

8. Conclusion

Nous avons montré qu’il existe deux catégories de vocabulaire : celui spécifique à l’application et celui, plus général, utilisable quel que soit le problème traité.

Le vocabulaire spécifique peut cependant être organisé autour d’un certain nombre de grandes idées si on admet que les applications utilisent des techniques globalement communes.

Le vocabulaire général est pris soit parmi les termes classiques de la CAO soit parmi les termes spécifiques de la description et de la conception d’images de synthèse. Comme le soulignent aussi [Dem94], [Dan95] et [DaL96], il est possible d’utiliser un vocabulaire adimensionnel et imagé. Le problème consiste alors à bien l’interpréter, c’est-à-dire à considérer des formes ou des concepts communéments admis, en limitant les ambiguïtés. Ceci est aussi valable, plus généralement, pour tout le vocabulaire commun que nous avons indiqué. L’essentiel est, en effet, de définir un ensemble de mots les mieux interprétés possibles par un maximum de personnes.

Nous avons vu aussi que l’interprétation d’une description et la gestion de la cohérence sont des problèmes difficiles à traiter.

Enfin, pour rendre la description aussi fiable que possible, il est important d’une part de donner toutes les possibilités de dialogue à l’utilisateur et d’autre part, de structurer correctement les descriptions complexes.

Toute cette étude à donnée naissance à l’idée qu’il est indispensable de mettre en place un formalisme de représentation et de gestion des propriétés souple, formel et unique. Nous avons donc travailler sur ce thème. La partie II propose un formalisme basé sur les ensembles flous et reprenant un grand nombre de caractéristiques des études en modélisation déclarative. Nous avons aussi proposé une classification des propriétés que l’on retrouve dans [DeM97] et dans le chapitre II.4.

Nous allons étudier maintenant les techniques permettant, à partir de cette description, de générer l’ensemble des scènes possibles (si possible toutes).

Chapitre I.3
Calcul des solutions

1. Introduction

Une fois la description terminée, il faut rechercher les formes de l’univers qui y répondent. L’objectif est de passer du modèle abstrait, défini par les propriétés (plusieurs formes peuvent répondre à ce modèle), à une collection de modèles géométriques, chacun définissant une forme (unique).

Pour cela, plusieurs algorithmes peuvent être utilisés : des algorithmes spécifiques (section 2), la génération aléatoire et la résolution de contraintes (section 3), le parcours de l’arbre d’exploration (section 4) ou celui de l’arbre de génération (section 5).

Figure 6. Processus de génération [Ple91]

Remarque : La classification des algorithmes de génération proposée dans ce chapitre correspond à celle communément retenue en modélisation déclarative. Elle est basée essentiellement sur les types algorithmes utilisés pour la phase de calcul (tirage aléatoire et gestion de contraintes, arbres d’exploration ou moteurs d’inférence). Nous verrons dans la partie III que nous préférerons un mode de classement un peu différent basé sur les modes de génération : par énumération et par échantillonnage. Nous nous intéressons plus au comportement de l’algorithme que sur son implémentation.

2. Algorithmes spécifiques

Ces algorithmes sont adaptés au type d’objet qu’on veut construire. Ils sont efficaces mais ne permettent pas de structurer l’univers de formes ([LMM89]).

Nous trouvons cependant un exemple récent d’algorithme spécifique de génération. [Sir97] génère, à partir d’une description, une forme géométrique contenant toutes les solutions et uniquement les solutions. Dans son projet Solimac, il tente de déterminer les actions à effectuer pour qu’une partie d’une construction ou d’un ensemble de constructions soit au soleil (ou à l’ombre) durant une plage horaire à une saison donnée. Pour cela, il construit une pyramide d’ensoleillement qui délimite la zone de l’espace à prendre en compte. Elle est calculée à l’aide d’un algorithme spécifique. Lorsque la partie de bâtiment doit être au soleil, la solution est obtenue par découpage direct. Par contre, lorsqu’elle doit être au soleil, il existe une infinité de facettes « pare-soleil » (intersections entre les plans de l’espace et la pyramide).

3. Tirages aléatoires et système de contraintes

3.1. Introduction

Cette technique est utilisée lorsqu’il est possible de paramétrer les objets à engendrer. Le générateur tire des valeurs “au hasard” dans les intervalles de validité des paramètres. Nous trouvons cette technique dans [Ple91], [Chau92-94], [Don93], [Paj94b], [Pou94a], [Mou94] et [Dem94] par exemple.

Il est possible de distinguer deux méthodes :

1. Le tirage aléatoire sans contrôle. Il utilise seulement un générateur pseudo-aléatoire sans chercher à vérifier une quelconque loi de probabilité. Cette méthode est simple mais il n’est pas possible de tirer des informations sur les objets engendrés.

2. Le tirage aléatoire sous contrôle. Il fixe une loi de probabilité à l’avance ([Chau92-94] utilise une loi normale).

Après avoir exposé les principe de la méthode de tirage aléatoire sous contrôle, nous présenterons l’exemple de celle proposée par [Chau94]. Nous montrerons ensuite que ces méthodes s’oriente actuellement vers les CSP (Constraint Satisfaction Problem).

3.2. Principe

Globalement, un système à tirage aléatoire sous contrôle ([Mou94] appelle cela la modélisation déclarative interactive) fonctionne de la manière suivante : détermination des intervalles de validité des différents paramètres et tirage des valeurs. Les intervalles sont déterminés en fonction des descripteurs utilisés, des quantificateurs et des valeurs par défaut. Des optimisations sont opérées pour réduire ces domaines. Tout au long de la génération, les intervalles sont réduits grâce à des opérations en fonction des contraintes posées (arithmétique des intervalles) et des valeurs déjà déterminées (vérification en avant).

[Ple91] propose un système de résolution de contraintes. Il est basé sur une organisation hiérarchique. Il parcourt l’arbre syntaxique de la description pour récupérer toutes les contraintes. Puis, soit par héritage, soit par synthèse, il construit le système. La résolution peut être faite soit globalement (sur toutes les contraintes) soit localement (sur les contraintes d’un nœud). Enfin, après l’avoir simplifié, il le résout en prenant toutes les valeurs possibles. Cependant, les contraintes qu’il gère sont uniquement des équations. Les inéquations sont utilisées pour les vérifications des valeurs trouvées. Les systèmes d’équations sont donc assez simples. Cette solution est reprise et optimisée par [Tam95].

3.3. Exemple : la méthode proposée par [Chau94]

Nous allons maintenant regarder plus en détail l’évaluation d’une description dans l’optique d’un traitement par échantillon en tirage aléatoire sous contrôle. Cette méthode est proposée par [Chau92-94]. Ici, toutes les contraintes sont traitées de la même manière qu’elles soient des équations ou des inéquations. Les systèmes sont aussi bien linéaires qu’hyperboliques.

3.3.1 Evaluation d’une description absolue

Une description absolue est une description ne comportant que des propriétés absolues (sans aucune référence à d’autres objets de la scène). C’est une conjonction de propriétés absolues. Cette situation est la plus simple. Pour chaque paramètre, il faut déduire l’intervalle intersection des intervalles par défaut et des différentes contraintes imposées par la description. La valeur du paramètre est obtenue par tirage aléatoire dans cet intervalle (appelé aussi intervalle résultat).

3.3.2 Evaluation d’une description relative

Une description relative est une description comportant au moins une propriété relative, c’est-à-dire au moins une propriété faisant référence à un autre objet de la scène. En plus du traitement que nous venons de voir pour les descriptions absolues, les descriptions relatives demandent un traitement particulier. En effet, les contraintes ne portent plus sur un seul paramètre mais sur plusieurs. De plus, elle ne sont pas forcément linéaires.

3.3.3 Traitement d’une description relative

Les propriétés relatives introduisent, en plus des intervalles par défaut ou déterminés par les propriétés absolues, des contraintes (équations ou inéquations) portant sur un ou plusieurs paramètres. Le traitement permet de déterminer les intervalles résultats et les contraintes sur les paramètres. L’objectif est alors de résoudre un système d’équations et d’inéquations tout en respectant les intervalles résultats.

Les contraintes sont prises en compte lors de la détermination d’une valeur d’un paramètre. Les valeurs sont recherchées dans l’espace à n dimensions (pour des contraintes portant sur n paramètres). L’objectif est de rechercher le sous-espace respectant la ou les contraintes. Ensuite, un des paramètres est tiré aléatoirement. Ceci fixe une des dimensions et le traitement est relancé sur un espace à n-1 dimensions.

Souvent, l’espace est constitué de composantes connexes. Pour choisir une solution assez différente de la précédente, il suffit alors de choisir le tirage dans une autre composante.

Dans certains cas, il existe aussi des algorithmes dits “de recherche opérationnelle” traitant parfaitement bien les problèmes. Il y a, entre autres, l’algorithme du simplexe (utilisé par [Mou94])... [Chau94] montre dans son étude bibliographique qu’il existe un certain nombre de techniques concernant la géométrie sous contraintes qui proposent des résolveurs de systèmes de contraintes. Mais, elle montre que ces systèmes ne sont pas totalement adaptés à la modélisation déclarative.

En effet, ils ont les inconvénients suivants :

· Les contraintes sont d’un type trop particulier.

· Une seule solution est fournie.

· Dans le cas où toutes les solutions sont produites, on ne peut pas contrôler l’ordre d’obtention.

· Si la description est incohérente, il n’y a pas de gestion de compromis.

Seule une méthode proposée par Snyder ([Sny92]) parait utilisable, mais elle nécessite la mise en œuvre d’un interpréteur de fonctions d’intervalle. C’est cette solution que propose [Chau94] en l’adaptant à la modélisation déclarative. Cette méthode permet de traiter des contraintes simples (linéaires) mais aussi des contraintes plus complexes (hyperboliques).

3.3.4 Traitement de la cohérence

Parfois, les intervalles correspondant aux contraintes imposées à un paramètre sont disjoints. Nous avons alors une contradiction.

Une contradiction peut se résoudre de trois manières :

1. Résoudre dans un ordre donné et laisser tomber les propriétés qui ne peuvent pas être satisfaites. On abandonne l’intervalle disjoint par rapport à l’intervalle résultat courant. Une conséquence de cette solution est que l’ordre de parcours devient très important. Elle donne la priorité à l’obtention d’un objet plutôt qu’aux paramètres. Ceci favorise ce qui est décrit en premier. C’est une solution “coûte que coûte”. Il est possible de donner à l’utilisateur l’information sur le conflit (entre autres, les propriétés abandonnées).

2. Proposer un compromis. Le système détermine une solution intermédiaire.

3. Proposer à l’utilisateur d’effectuer un choix entre les contraintes conflictuelles. La résolution du conflit est alors sous sa responsabilité.

Dans le cas où l’on tente un compromis, deux solutions sont envisageables :

1. On prend la moyenne entre les deux intervalles dont l’intersection est vide. La valeur obtenue ne satisfait alors aucun des deux (cela privilégie plutôt les dernières propriétés).

2. On prend la valeur de l’intervalle résultat la plus proche de la propriété conflictuelle.

Cette méthode ne gère les problèmes de cohérence que lors du traitement numérique. [Don93] propose d’étudier la cohérence et de simplifier le système d’équations par un pré-traitement logique. Il se place, comme [Chau94], dans le cadre des propriétés de type spatial (placement et positionnement). Les relations permettent de construire trois graphes de contraintes basés sur la logique de Allen selon les trois dimensions de l’espace. Les graphes sont simplifiés et permettent de mettre en évidence un certain nombre d’incohérences. La résolution numérique se fait seulement après.

3.3.5 Structures de données

Pour les structures de données utilisées dans ce type de système, [Chau92] propose un objectif pour les modèles géométriques à utiliser : définir les objets de manière unique tout en privilégiant la séparation des paramètres (l’indépendance). Elle propose en particulier comme modèle pour ces boîtes, le modèle TPFO où les paramètres de Taille (paramètre particulier T donnant la taille du plus grand côté), de Place (coordonnées du centre de masses), de Forme (aT pour le côté intermédiaire et abT pour le plus petit côté) et d’Orientation (H pour l’horizontalité et S pour le sens) sont indépendants.

Remarque : ce modèle est intéressant pour manipuler les boîtes englobantes des objets mais ne concerne que des propriétés de positionnement dans l’espace et de forme pour des boîtes parallépipédiques.

En ce qui concerne la représentation de la description, [Chau94] propose la notion de Table Sémantique. Une table sémantique est composée de la liste des paramètres, de leurs caractéristiques, des intervalles qui leurs sont associés et de la liste des contraintes posées par la description. Dans le cas d’une conjonction de propriétés, le traitement consistera à obtenir une table sémantique résultat à partir de chacune des tables sémantiques des propriétés. Dans le cas d’une disjonction, le résultat sera une table sémantique parmi celles correspondant à chaque propriété de la disjonction.

3.4. Vers les CSP

Actuellement, les méthodes de tirage aléatoire sous contrôle s’orientent nettement vers les techniques de résolution de contraintes de type CSP (Constraint Satisfaction Problem ; [Fron94]).

En effet, [Don93] et [Chau94] puis, plus récemment, [MaM96] s’intéressent de près à l’optimisation du traitement des contraintes en utilisant l’arithmétique de intervalles (calculs sur les intervalles à partir, comme nous l’avons vu, de fonctions d’intervalle).

[Lie96] et [Cham97] utilisent des techniques CSP classiques sur le parcours et la réduction de domaines (souvent des intervalles) comme les vérifications en avant (« lookahead »). Ils utilisent ainsi des techniques d’optimisation classiques telles que l’ordonnancement des variables à explorer…

Pour plus de détails sur ces techniques, on pourra se référer à [ChM94a], [Chau94], [Fron94] et [Lie96].

3.5. Conclusion

Ces techniques n’assurent pas que toutes les formes solutions de l’univers sont atteintes et, notamment, LA solution attendue par l’utilisateur.

Souvent, ces systèmes ne proposent qu’une seule solution. L’utilisateur peut néanmoins, si elle ne lui plaît pas, en demander une autre. Cependant, la nouvelle solution n’aura pas forcément de rapport avec la précédente ou risque d’avoir déjà été rencontrée. Il risque donc de chercher longtemps LA solution. Il n’est pas possible de diriger les recherches. Par contre, il peut modifier une bonne solution afin de tendre vers LA solution (notion d’ébauche).

Cette technique est intéressante si l’on s’intéresse à un univers infini car, de toute manière, il n’est pas possible de voir toutes les solutions. Donc elle semble adaptée pour des univers où les valeurs des paramètres sont prises soit sur des domaines infinis soit sur des intervalles continus.

Nous pouvons faire quelques remarques :

· Cette technique n’est intéressante que si l’application possède suffisamment de propriétés paramétrables (propriétés mesurables et paramétrables, paramètres sur des intervalles facilement déterminables, bornés et continus). En effet, les formes solutions seront générées à partir de tirages sur les intervalles de définition des paramètres. Si le nombre de propriétés paramétrables n’est pas suffisamment important, il va falloir faire de très nombreux tirages avant de trouver une solution. Le temps pour l’obtenir risque d’être très important surtout si les relations entre les paramètres et les répartitions des valeurs sur les intervalles ne sont pas maîtrisées.

· Très souvent, les intervalles de validité des paramètres sont divisés afin de rendre compte des qualificatifs possibles de la propriété associée. Ces divisions constituent des sous-intervalles réguliers, le plus souvent disjoints et fixés définitivement. Elles sont arbitraires et donc pas forcément judicieuses du point de vue de l’utilisateur.

· La fonction fournissant une valeur aléatoire revêt une grande importance si elle doit être utilisée. En effet, il peut être intéressant de conserver des informations pour effectuer plusieurs fois une génération identique (comme par exemple pour tester l’influence d’une règle d’optimisation sur un moteur d’inférence). Dans ce cas, le mécanisme de génération aléatoire doit fournir les mêmes séquences aléatoires lors de deux générations successives. Ceci est la plupart du temps possible car le mécanisme de génération fournit des valeurs à partir d’un germe qu’il suffit de mémoriser pour obtenir deux fois de suite des séquences identiques. Lorsque ce n’est pas le cas, il faut implémenter un mécanisme interne de génération aléatoire (basé le plus souvent sur des fonctions trigonométriques) de manière à disposer de ce germe.

[Chau92-94], [Dem94], [Paj94b], [Pou94a] (entre autres) choisissent de générer une solution sous contraintes en laissant à l’utilisateur la possibilité de la modifier (à l’aide d’un vocabulaire spécifique). Cela permet d’obtenir rapidement une solution grossière puis de l’améliorer par retouches successives. Nous avons alors une modification déclarative. Nous reverrons cela dans un prochain chapitre.

4. Arbres d’exploration

4.1. Introduction

Lorsque l’univers des formes est dénombrable (les valeurs sont choisies sur des intervalles discrets) et fini naturellement (les valeurs sont dans des intervalles bornés) ou, le plus souvent, artificiellement (la profondeur de l’arbre est, par exemple, limitée), il est possible de construire un ou plusieurs arbres permettant une énumération totale ou partielle de l’univers (technique étudiée et utilisée par [Col88], [Elk89], [Ker89], [Col90a], [Mar90a], [Mar90b], [Pas90], [Pou94], [Paj94] et [Fau95]). Ces arbres sont appelés arbres d’exploration (arbres de modélisation pour [Elk89]). Tous les arbres ne permettent pas d’atteindre toutes les solutions.

4.2. Formes partielles et formes complètes

Lors du parcours de l’arbre, nous allons obtenir des formes qui ne sont pas totalement construites appelées formes partielles, et des formes totalement construites appelées formes complètes. Les formes complètes se trouvent forcément sur les feuilles (nœuds ne possédant pas de fils) mais elles peuvent aussi se trouver aussi sur les autres nœuds.

Pour certaines applications ([Col90]) tout nœud est une forme complète. C’est souvent le cas pour les arbres générant des formes constituées d’objets élémentaires identiques du point de vue de leur utilisation.

Remarque : Les éléments peuvent être différents par rapport à certains paramètres qui les définissent (couleur, orientation, nombre de faces). De plus, toutes les combinaisons ne sont pas forcément autorisées

Par exemple, les applications suivantes sont dans ce cas :

· [Pou94] avec les voxels ;

· [Paj94] avec les segments ;

· [Col90] avec les polyèdres...

4.3. Élagages

Le nombre de formes à étudier peut être très important (c’est un problème essentiel de cette méthode). Il est donc intéressant de mettre au point un système d’élagage afin d’éliminer les branches de l’arbre qui produiront des formes ne répondant pas au système de propriétés, c’est-à-dire à la description de l’utilisateur.

Les techniques d’élagage ont été étudiées par [Elk89], [Pas90], [Col88], [Col90a], [Col92], [Mar90], [Paj94] et [Pou94]. Ils se sont basés sur les caractéristiques de comportement des propriétés ainsi que sur certaines relations entre elles.

Il existe deux types d’élagage :

1. L’élagage immédiat, appelé aussi élagage par le haut. Lorsqu’une forme possède une propriété définitivement vérifiée qui n’est pas cohérente, cette forme est rejetée et le parcours de cette branche s’arrête là. Cet élagage peut avoir lieu aussi lors d’une vérification définitive de toutes les propriétés (Voir les réduction des contrôles). Il est donc effectué quand le système est certain de l’échec ou de la réussite de toutes les formes du sous-arbre.

2. L’élagage par le bas. Lorsqu’une propriété requise ne peut plus être vérifiée dans le sous-arbre du nœud courant, il n’est plus nécessaire de continuer le parcours de cette branche. Aucune forme issue de ce nœud ne sera solution. On opère donc un élagage sous la forme courante, l’objectif ne pouvant être atteint.

Remarque : Souvent, pour effectuer un élagage par le bas, le système doit posséder au moins une propriété prédictible (possède une mesure permettant de prédire le prochain niveau où elle sera vérifiée) et connaître la profondeur du sous-arbre restant à parcourir ce qui n’est pas toujours évident. Cela dépend, en réalité, de l’arbre d’exploration utilisé et des propriétés demandées.

4.4. Réduction des contrôles

La réduction des contrôles ([Col90a]) ou stérilisation des propriétés ([Gra96]) est une diminution du nombre de propriétés à étudier. Là aussi, elle est basée sur certaines caractéristiques des propriétés. Elle a lieu quand une propriété stable requise est détectée. Cette propriété est retirée de la liste des propriétés à vérifier pour toutes les branches issues de la forme courante car elle sera toujours vérifiée. Toutes les formes issues du nœud héritent de la propriété.

Lorsqu’on est sûr qu’une propriété ne sera pas vérifiée au moins avant un niveau n du parcours de l’arbre, il n’est pas nécessaire de vérifier les propriétés de la liste avant ce niveau. Il va donc y avoir une réduction globale des contrôles ou stérilisation globale des propriétés : aucune propriété ne sera plus étudiée avant le niveau n. Ce type de réduction peut avoir lieu plusieurs fois dans le parcours d’une branche. Seulement, elle n’est utilisable que grâce à des propriétés applicables sur les formes complètes.

Remarque : Pendant la construction d’une forme, il peut arriver que toutes les propriétés soient stables et vérifiées. Grâce à la réduction des contrôles, il n’y a plus alors de propriétés à vérifier dans la liste des propriétés. Nous avons alors une forme partielle dont toutes les descendantes sont des formes solutions. Il n’est alors plus nécessaire de continuer le parcours de l’arbre. Nous avons alors un élagage immédiat. Cependant, le sous-arbre est conservé pour être exploité au niveau de la prise de connaissance.

4.5. Différentes caractéristiques des propriétés

4.5.1 Les caractéristiques propres

Pour [Col90a-92] il existe deux grands types de propriétés :

1. Les propriétés “simples” ou propriétés qualitatives. Pour une forme donnée, elles déterminent directement si la forme possède la propriété.

2. Les propriétés mesurables ou propriétés quantitatives. Elles possèdent une fonction de mesure d’une forme (qui peut être croissante, décroissante, monotone ou quelconque). A partir de cette mesure, elles déterminent si la forme possède la propriété.

Pour [Paj94b] toute propriété peut être décomposée en deux parties :

1. la mesure d’une quantité associée à une ou plusieurs caractéristiques de la forme (le type de la mesure peut alors être booléen, entier, réel...),

2. une qualification par rapport à cette mesure notée à l’aide des opérateurs “<“, “>”, “=”, “≤”, “≥” et “≠”.

Les propriétés peuvent être de deux catégories suivant leur champ d’application :

1. Les propriétés locales. Elles sont vérifiées sur un ou plusieurs éléments de la forme.

2. Les propriétés globales. Elles sont vérifiées sur l’ensemble de la forme (Il existe aussi des propriétés globales qui sont des mesures de pourcentage de vérification d’une ou plusieurs propriétés locales sur la forme.).

Les notions de propriétés locales et globales ont déjà été rencontrées dans le chapitre I.2 à propos du vocabulaire utilisé et de la structure de la description. Nous montrerons dans le chapitre II.4 que cette classification classique n’est pas satisfaisante et nous proposerons une autre définition pour « propriété locale » et « propriété globale ».

[Col90a-92] détermine aussi des relations entre une propriété et sa négation. Il propose, par exemple, la règle suivante : si P provoque une réduction des contrôles (resp., un élagage par le bas) alors ¬P provoque un élagage par le bas (resp., une réduction des contrôles).

Il détermine surtout des relations entre des propriétés différentes :

· Une propriété P’ est une sur-propriété d’une propriété P si elle est vérifiée au moins à chaque fois que P est vérifiée.

· P’ est une sous-propriété de P si elle n’est vérifiée que lorsque P est vérifiée.

Ces deux relations permettent d’améliorer les réductions des contrôles en éliminant plus de propriétés dans la liste des propriétés et permettent aussi de simplifier certaines détections d’élagage.

[Col90a-92] définit un ensemble de “théorèmes” permettant de déduire des sur-propriétés ou des sous-propriétés d’une propriété donnée.

Par exemple, on a :

· Si P’ est une sur-propriété de P et que P’ entraîne un élagage alors P entraîne aussi un élagage.

· Si P’ est une sous-propriété de P et que P’ entraîne une réduction des contrôles alors P entraîne aussi une réduction des contrôles.

Il indique aussi des situations permettant de dire si une propriété donnée est une sur-propriété ou une sous-propriété d’une autre.

4.5.2 Comportements lors d’un parcours d’une branche d’un arbre

[Col90a-92] classe les propriétés en trois ensembles selon leur comportement dans l’arbre d’exploration :

1. Les propriétés stables. Lors d’un parcours de l’arbre, dès que la propriété est vérifiée, elle le reste dans tout le sous-arbre issu du nœud courant. Si la propriété est requise, elle est alors supprimée de la liste des propriétés (R.d.C) ; sinon, elle provoque un élagage immédiat de l’arbre.

2. Les propriétés p-périodiques. Elles sont vérifiées périodiquement lors du parcours de l’arbre. La connaissance de la période permet d’opérer des élagages par le bas, si la profondeur de l’arbre est inférieure à la période, ou une réduction globale des contrôles.

3. Les propriétés prévisibles (ou prédictibles pour [Pou94b]). Leur comportement est connu à l’avance. Elles permettent de dire si des formes futures posséderont ces propriétés.

[Col90] met en évidence deux cas particuliers de propriétés p-périodiques :

1. les propriétés alternes (de période 2) ;

2. les propriétés p-régulières (entre deux périodes, elles ne sont pas vérifiées).

[Elk89] et [Pou94b] proposent une définition plus large des propriétés stables : une propriété est dite stable si elle est dans un état (vrai ou faux) au début de la génération de l’arbre et que, en cours de génération, si elle change une fois d’état, elle ne change plus d’état dans les niveaux inférieurs.

Il est important de noter que les caractéristiques des propriétés (stables, p-périodiques...) sont vérifiées pour un arbre donné et pas forcément pour tous.

[Pou94b] propose aussi la notion de propriétés pseudo-stables : une propriété est pseudo-stable si elle devient stable à une étape donnée de la génération, c’est-à-dire qu’elle peut passer un nombre quelconque de fois de l’état vrai à l’état faux (et vice-versa) mais qu’à partir d’une étape de la génération, elle se stabilise et n’évolue plus. On suppose que l’étape de stabilisation arrive avant les feuilles de l’arbre sinon toutes les propriétés seraient pseudo-stables.

Les propriétés stables, p-périodiques et pseudo-stables sont des cas particuliers de propriétés prévisibles (ou prédictibles).

[Paj94b] propose 4 classes de propriétés qui sont :

· les propriétés transmissibles de type 1 et de type 2 (identiques aux propriétés stables de [Pou94b]) ;

· les propriétés semi-transmissibles de type 1 et de type 2.

Les propriétés transmissibles de type 2 sont équivalentes aux propriétés stables selon [Col90b-92], [Elk89] et [Pou94b]. Les propriétés transmissibles de type 1 sont des propriétés qui, une fois non vérifiées, le restent dans tout le sous-arbre. Elle sont stables selon [Pou94b]. C’est, en quelque sorte, le “négatif” d’une propriété transmissible de type 2 (“négatif” d’une propriété stable selon [Col90b-92]).

Les propriétés semi-transmissibles ont la caractéristique de devenir stables seulement au second changement. Les propriétés semi-transmissibles de type 1 ne deviennent définitivement non vérifiées qu’après avoir été vérifiées. De même, celles de type 2 deviennent définitivement vérifiées qu’après avoir été non vérifiées.

Ces classes de propriétés sont gérées comme des propriétés transmissibles après leur premier changement de valeur. Dès qu’une propriété semi-transmissible de type 1 (resp. de type 2) devient vérifiée (resp. non vérifiée), elle sera étudiée dans tout le sous-arbre comme une propriété transmissible de type 1 (resp. de type 2) c’est-à-dire qu’elle permettra de mettre en place des élagages et des réductions des contrôles comme une propriété transmissible.

[Paj94b] montre aussi que toute propriété dont la mesure est monotone est forcément soit transmissible (pour les qualifications “<“, “>”, “≤” et “≥”) soit semi-transmissible (pour les qualifications “=” et “≠”).

L’objectif essentiel de ces relations est de se ramener à des propriétés stables (ou transmissibles) afin d’avoir des occasions d’élagage et de réduction des contrôles plus nombreuses et plus faciles à détecter.

[Mar90a-b] propose un classement des propriétés en 7 catégories :

1) La propriété ne peut être vérifiée que sur un objet complètement construit (sur une forme complète). Elle ne sera évaluée que sur une forme complète.

2) La propriété peut être vérifiée sur un objet partiellement construit (sur une forme partielle). De plus, une fois vérifiée, elle le reste (stable pour [Col90] et transmissible de type 2 pour [Paj94]). Elle peut faire l’objet d’une réduction des contrôles ou provoquer un élagage immédiat.

3) La propriété peut être vérifiée sur une forme partielle. De plus, une fois non vérifiée, elle le reste (stable pour [Pou94b], transmissible de type 1 pour [Paj94] et la négation d’une propriété stable de [Col90]). Elle peut provoquer un élagage immédiat de l’arbre ou faire l’objet d’une réduction des contrôles.

4) La propriété peut être vérifiée sur une forme partielle. De plus, une fois vérifiée, elle le reste sous certaines conditions de construction. Elle peut permettre de diriger la construction des formes.

5) La propriété peut être vérifiée sur une forme partielle. De plus, une fois vérifiée, elle l’est de façon périodique. Elle n’est pas vérifiée entre deux périodes. Elle n’est donc vérifiée qu’une fois par période (Pour [Col90] la propriété est p-régulière et p-alterne si la période est de 2). Elle peut permettre de mettre en place une réduction globale des contrôles (les propriétés ne sont vérifiées qu’à chaque période) entre chaque période de la propriété ou de provoquer un élagage par le bas si on peut affirmer qu’elle ne sera plus vérifiée (la longueur de la branche à parcourir étant inférieure à une période).

6) La propriété peut être vérifiée sur une forme partielle. De plus, une fois vérifiée, elle l’est de façon périodique. Elle peut être vérifiée entre deux périodes (p-périodique pour [Col90]). Elle est vérifiée au moins toutes les périodes.

7) La propriété peut être vérifiée sur une forme partielle. De plus, une fois vérifiée ou non, elle ne reste pas obligatoirement dans cet état par la suite. Elle n’est donc vérifiée que sur les formes complètement construites.

4.5.3 Résumé de différents comportements de certaines propriétés prédictibles

Les propriétés sont évaluées selon la logique booléenne classique. Donc, lors d’un parcours dans une branche d’un arbre, une propriété peut prendre deux états :

1. V (la propriété est vérifiée) ;

2. F (la propriété n’est pas vérifiée).

Il y a donc deux situations possibles liées aux deux états :

1. E (la propriété est étudiée et est V ou F) ;

2. ? (il n’y a pas de vérifications).

Un parcours de branche s’écrit alors à l’aide de la suite des états de la propriété. Par exemple : FFVVFFVFFVVVFF.

Pour synthétiser l’écriture d’un parcours, nous posons les éléments suivants :

· E* : l’état E se répète 0, 1 ou plusieurs fois ;

· E+: l’état E se répète 1 ou plusieurs fois ;

· E[p] : l’état E se répète p fois ;

· (ABCD) : les états A, B, C, D forment un “motif” (qui peut se répéter).

A l’aide de ces conventions, le Tableau 1 effectue une synthèse des classements de propriétés proposées dans les différents travaux en modélisation déclarative

Tableau 1 : Types des propriétés classiques

[Col90] (C), [Elk89] (E) et [Pou94] (P)	[Paj94]	Catégorie selon [Mar90a]	Branche	Remarques
Stable (C, E et P)	Transmissible de type 2	2	F*V+
Stable (E et P)	Transmissible de type 1	3	V*F+	Extension de Stable pour (C)
p-régulière (C)		5	(VF[p-1])+
Alterne (C)		5	(VF)+
		5	F*(VF[p-1])+	Extension de p-régulière de (C)
		6	F*(VE[p-1])+	Extension de p-périodique de (C)
p-périodique (C)		6	(VE[p-1])+
		1 - 4 - 7	?*E+	Sans caractéristiques générales mais selon le domaine d’application des optimisations sont possibles
	Semi-transmissible de type 1		F*V+F+
	Semi-transmissible de type 2		V*F+V+
Pseudo-stable (P)			EF+V+ EV+F+	Extension des semi-transmissibles de [Paj94]
			F[p]V[q]F*	Propriétés pq-semi-transmissibles type 1 [Des95a]
			V[p]F[q]V*	Propriétés pq-semi-transmissibles type 2 [Des95a]

Remarques :

· Toutes ces catégories de propriétés sont regroupées dans l’ensemble des propriétés prévisibles (selon [Col90b-92]) ou prédictibles (selon [Pou94b]).

· Ces comportements sont valables pour un arbre donné et pas forcément pour tous.

· Une autre catégorie de propriétés, symétrique du point de vue du parcours dans une branche, existe. Elles ont le comportement suivant : F*V[p]F[q] ou V*F[p]V[q]. Cependant, elles n’apparaissent pas dans les applications et leur traitement semble moins simple.

4.6. Vérification des propriétés

La description de l’utilisateur génère une ou plusieurs listes de propriétés. Une liste de propriétés correspond à une conjonction de propriétés. La présence de plusieurs listes peut être la conséquence de disjonctions dans la description.

La vérification de l’exactitude des propriétés peut se faire à plusieurs moments (selon [Elk89], [Pas90] et [Col90b]) :

· Vérification dynamique. Les propriétés sont vérifiées au cours de la construction de chaque nœud c’est-à-dire aussi bien sur les formes complètes que sur les formes partielles. C’est cette solution qui permet la mise en place d’élagages et de réductions des contrôles. C’est le cas lors d’un parcours partiel de l’arbre d’exploration ([Col90a], [Mar90]...).

· Vérification a posteriori. Les propriétés ne sont vérifiées que sur les formes complètes. C’est le cas lors d’un parcours systématique de l’arbre d’exploration ou pour certaines propriétés (en particulier celles de catégorie 1). Pour ces dernières, une vérification en cours de construction est parfois possible sous certaines conditions (présence d’autres propriétés, adaptation du mode de génération...) mais certaines formes risquent alors de ne pas être générées (voir [Pou94a]).

· Vérification “de temps en temps”. Les propriétés ne sont vérifiées que de temps en temps ([Col90a]). Ceci est intéressant pour des propriétés stables très coûteuses. Si une propriété stable se trouve vérifiée sur un nœud donné, il va falloir alors vérifier toutes les propriétés stables pour tous les nœuds qui n’ont pas été vérifiés (qui ont été “oubliés”) depuis la dernière fois. Cette solution est aussi utilisée quand il y a des propriétés périodiques. L’intervalle entre deux vérifications peut être constant ou varier dynamiquement.

Il est parfois intéressant de faire une détection incrémentale d’une propriété lorsque le coût de l’étude sur la forme globale est très important ou que cette propriété est locale. La détection incrémentale prend en compte les modifications locales tout en considérant l’état courant. L’étude n’est pas effectuée sur la forme globale. Par contre, cette technique n’est pas compatible avec la réduction globale des contrôles. Il est absolument nécessaire de vérifier la propriété à chaque nœud même si une vérification a déjà échoué.

Habituellement, à chaque propriété est associée une procédure de vérification. L’étude (la vérification) d’une forme consiste à parcourir la liste des propriétés, les unes après les autres (sauf en cas de parallélisation), en appliquant à chaque fois la procédure de vérification. L’étude s’arrête quand toutes les propriétés ont été vérifiées (c’est alors une forme solution) où dès qu’une vérification échoue sauf dans le cas où il existe d’autres listes à étudier (dans ce cas on passe à la suivante). Comme les propriétés sont étudiées séquentiellement, il est important de pouvoir gérer l’ordre des propriétés dans cette liste.

L’idée de gérer l’ordre des propriétés est souvent avancée dans les différents projets mais aucune proposition n’a été faite.

Souvent, l’étude d’une propriété est assez coûteuse. [Ker89] propose de vérifier les propriétés d’une autre manière. Il part du principe que beaucoup de propriétés peuvent être exprimées comme une combinaison de propriétés élémentaires. Il est donc plus facile de les définir comme des règles d’inférence. Ainsi, il met en place un système expert. Le traitement d’une forme se déroulera comme une combinaison des modes déductifs et impératifs. L’étude des propriétés se déroule alors comme suit : tant que c’est possible, déduire toutes les propriétés possibles par saturation de la base puis appliquer l’étude impérative d’une propriété plus complexe et recommencer le traitement.

4.7. Les gardes

Pour éviter de vérifier trop souvent une propriété très coûteuse, il est possible de mettre en place des gardes permettant de dire si l’étude de la propriété a des chances de réussir [Col90a]. Ces gardes permettent aussi de gérer les vérifications périodiques.

Une garde est une condition de déclenchement pour une optimisation (étude d’une propriété) afin d’éviter trop d’études complexes. Si Q est une garde pour une propriété P, nous pouvons remarquer que P est vérifiée seulement si Q l’est. Par conséquent, Q est une sur-propriété de P.

Une garde est une sur-propriété de la propriété sur laquelle elle porte. La notion de garde est donc une application de la notion de sur-propriété.

Les gardes peuvent être de différentes catégories [Col90a] :

· Garde statique pour vérification systématique. La garde est toujours vraie. Elle sert pour les propriétés dont le coût d’étude est quasi-nul ou pour les détections incrémentales.

· Garde statique pour vérification périodique. La garde est vraie périodiquement pour les propriétés périodiques ou pour les propriétés stables très coûteuses qui peuvent être vérifiées à tout moment.

· Garde statique à vérification non périodique. La garde dépend d’une fonction qui définit l’intervalle d’étude. Cette fonction est indépendante des formes. Elle permet d’augmenter le nombre d’études au moment où elles ont le plus de chance de réussir. Elle permet de gérer une sorte de réduction des contrôles pour certaines propriétés qui ne peuvent être vérifiées qu’à partir d’un niveau donné ou jusqu’à un niveau donné et permet d’augmenter (resp. diminuer) les études au fur et à mesure que la probabilité de réussite est plus (resp. moins) grande.

· Garde dynamique. La prochaine forme à étudier est fonction de la forme courante. Elle permet un réglage optimal des intervalles.

4.8. Parcours systématique d’un arbre d’exploration

Le parcours élémentaire d’un arbre d’exploration est le parcours systématique. Toutes les formes possibles de l’univers sont construites et la vérification se fait a posteriori sur les formes complètes. L’arbre est parcouru en profondeur d’abord avec un traitement préfixé (l’étude du nœud se fait en premier lieu). Cette solution est excessivement coûteuse du fait du très grand nombre de solutions générées.

4.9. Parcours partiel d’un arbre d’exploration

La solution au problème du nombre de solutions est d’effectuer un parcours partiel de l’arbre d’exploration (voir [Col90a] et [Mar90]). Le but est de provoquer le maximum d’élagages et de réductions des contrôles possibles en utilisant principalement les propriétés stables et périodiques. Les vérifications sont incrémentales, “de temps en temps” ou dynamiques. Les propriétés sont gardées.

Algorithme 1. Le parcours partiel a la forme

Algorithme Parcours(Forme courante, liste des propriétés, Liste d’éléments)

/* Etude de la forme */

Vérifier la Forme courante avec la liste des propriétés si nécessaire

Si Forme courante est solution et Forme complète Alors

l’étudier et la conserver

Fin Si

/* Génération des branches si nœud */

Si nœud ≠ Feuille Et Pas d’élagage Alors

Générer toutes les Formes possibles

avec la liste d’éléments disponibles et la Forme courante

Appliquer Parcours(...) sur ces Formes possibles

/* Cas où vérifs périodiques */

Revérifier la Forme courante si besoin

Si Modifications Et

Forme courante est solution Et

Forme complète Alors

l’étudier et la conserver

Fin Si

Fin Algorithme Parcours

4.10. Parcours dirigé d’un arbre d’exploration

[Col90a] propose encore une amélioration au parcours partiel de l’arbre d’exploration : le parcours dirigé. L’idée est de diriger l’exploration de l’arbre de façon à ne pas engendrer des formes vouées a priori à l’échec. Pour cela, le système doit pouvoir gérer les erreurs de manière à reconnaître les situations qui ont mené à l’échec. Il doit être possible de reconnaître les conditions qui donneront une propriété déjà vue et de connaître les opérations élémentaires qui permettent soit d’obtenir soit de conserver certaines propriétés requises. Pour ce type de parcours, les propriétés de catégorie 4 sont très utiles.

4.11. Familles d’arbres d’exploration

Les arbres, nous l’avons vu, peuvent être différents selon l’application et les choix réalisés (type de parcours...). Ils peuvent être classés selon la méthode de construction.

4.11.1 Techniques de génération

Ils peuvent être répartis dans deux familles [Mar90a] :

1. Les arbres simples. Chaque fils est construit par une seule opération élémentaire effectuée sur le nœud courant.

2. Les arbres à valuations multiples. Un fils est construit à l’aide d’une combinaison d’opérations élémentaires. Cette famille d’arbres est très intéressante du point de vue conceptuel mais très difficile à mettre en place du point de vue pratique. La mise au point des techniques d’élagage et de réduction des contrôles est très complexe et demande à être approfondie. Elle permet cependant de construire, dans certaines conditions, des fils de telle manière que certaines propriétés seront, à coup sûr, conservées (par exemple, maintient de symétries).

Suivant les applications et les objectifs des concepteurs, les arbres de génération utilisés sont différents et très souvent fortement dépendent de l’application.

Cependant, quelques techniques générales apparaissent :

· Les arbres d’énumération. Nous étudierons cette technique dans un prochain paragraphe et dans l’annexe 4. Ils sont souvent utilisés d’une manière implicite.

· Les arbres de paramètres. Quand l’objectif est de générer un objet entièrement défini par un ensemble de paramètres pris sur des intervalles bornés, il est possible de mettre en place un arbre où les fils du niveau “i” sont créés pour toutes les valeurs possibles du paramètres “i+1” (cette technique est utilisée, par exemple, par [Fau95] pour générer un plan dans l’espace). Il est alors important de bien choisir l’ordre des paramètres afin de ne générer qu’un minimum de formes.

4.11.2 Arbres constructifs et arbres destructifs

La plupart des applications ([Mar90], [Col90], [MaM89-94]...) utilisent des arbres de type constructif c’est-à-dire qu’un fils est obtenu en ajoutant ou modifiant des éléments au père.

Mais il est possible aussi, de mettre en place des algorithmes destructifs. A partir d’une forme donnée, ils produisent les différentes formes par modifications et destructions successives (comme le ferait un sculpteur sur un bloc de pierre). C’est ce que propose [Ker89]. A partir du triplombre, il construit l’objet dit “maximal” (unique) puis génère toutes les solutions par suppression des voxels inutiles. Il propose aussi, par cette technique, la possibilité de créer des cavités ou des creux (par “creusage”) et des formes circulaires (par “fraisage”).

[Elk89] propose d’utiliser, suivant la situation, soit une technique constructive soit une technique destructive. Les deux techniques sont dites duales. [Pou94b] utilise ce principe pour la génération des matrices de voxels. S’il arrive à montrer que les formes solutions sont plus proches de la matrice vide, il utilisera une technique constructive : il partira d’une matrice vide, la construction se fera par ajouts de voxels pleins. Par contre, s’il peut montrer que les solutions sont proches de la matrice pleine, il utilisera une technique destructive : il partira d’une matrice pleine, la destruction se fera par suppressions de voxels pleins. La notion de proximité correspond, pour lui, à la profondeur nécessaire pour obtenir une solution c’est-à-dire au nombre de voxels à modifier.

Par contre, il n’est pas possible de mélanger les techniques constructives et destructives car l’arbre de génération deviendrait un graphe et ne serait pratiquement pas exploitable.

4.12. Arbres et ensembles de formes

Les arbres sont aussi classés selon l’ensemble des formes qu’ils génèrent. Ils peuvent être de deux catégories [Col90] :

1. les arbres complets où toutes les formes de l’univers sont générées ;

2. les arbres partiels où seulement un sous-ensemble de formes est généré.

Nous pouvons remarquer qu’il existe un certain nombre d‘ensembles de formes : l’ensemble U des formes de l’univers (toutes les formes possibles) qui est l’ensemble des formes générées par l’arbre systématique, l’ensemble F des formes de l’arbre et l’ensemble S des formes solutions (formes vérifiant la liste des propriétés).

Nous allons avoir 4 catégories d’arbre partiel suivant l’ensemble des formes générées :

· Les arbres suffisants. Toutes les formes générées sont solutions mais l’ensemble des formes solutions n’est pas complet. D’autres formes solutions existent mais ne sont pas générées par cet arbre : F Ì S Ì U

· Les arbres nécessaires. L’ensemble des formes solutions se trouve dans l’arbre mais il en existe d’autres qui ne sont pas solutions : S Ì F Ì U

· Les arbres non fiables. Seules certaines formes sont solutions. Certaines formes solutions ne sont pas dans l’arbre : S Ç F ≠ Ø et S Ë F et F Ë S

· Les arbres incorrects. Aucune forme solution ne se trouve dans l’arbre : S Ç F º Ø

[Pou94b] propose aussi la notion d’arbre minimal. Cet arbre contient toutes les formes possibles de l’univers, sans répétitions.

Les arbres nécessaires et suffisants sont des arbres contenant uniquement toutes les formes solutions. Ils sont appelés aussi arbres triviaux. [Pou94b] montre qu’il est possible de construire de tels arbres en fonction d’une propriété donnée (mais ce n’est vrai que pour certaines propriétés bien particulières... et rares !). Toutes les formes générées par un tel arbre vérifient la propriété. Seulement, la plupart du temps, la description possède plusieurs propriétés. Il n’est alors pas possible de construire l’arbre trivial associé à cet ensemble de propriétés. Par contre, dans une description, s’il existe une ou plusieurs propriétés permettant de construire un tel arbre, il est possible de choisir l’arbre générant le moins de formes et/ou associé à la propriété la plus coûteuse. La propriété concernée est alors retirée de la liste des propriétés (réduction des contrôles) et les autres sont traitées normalement.

Le problème est de déterminer les propriétés (et les algorithmes associés) qui vont permettre ce genre d’arbre. Il est clair que toutes les propriétés ne peuvent prétendre être utilisables pour cette méthode. Une première caractéristique est de pouvoir construire directement une forme solution. Une fois la première obtenue, le passage vers les autres formes doit être relativement simple. Les catégories de propriétés qui facilitent la mise en place d’un tel traitement sont les catégories 2, 3, 4 et 5 (catégories selon [Mar90]). Globalement, les conditions qui permettent de dire si une propriété donnée pourra ou non être à l’origine d’un tel arbre demandent à être étudiées.

On pourrait appeler ce type d’arbre de génération spécifique un arbre 1-trivial. Par extension, nous appellerons l’arbre respectant systématiquement N propriétés de la liste un arbre N-trivial. Un arbre trivial est un arbre N-trivial où N est exactement égal au nombre de propriétés demandées par la description. Il faut noter que cette technique risque de se rapprocher des algorithmes spécifiques (avec les problèmes qui sont liés) car la génération dépend d’une ou plusieurs propriétés, souvent spécifiques à l’application.

4.13. Cas particulier : les arbres d’énumération

Cette technique de génération par arbres d’énumération est une technique de base. Elle est présentée par [LMM89] et [Elk89] et utilisée par [Mar90] et, plus particulièrement, par [Pas90], [Paj94b] et [Pou94b]. L’objectif principal est de générer des arbres minimaux, c’est-à-dire des arbres où toutes les formes sont différentes.

4.13.1 Principe

Cette technique se base sur un arbre d’énumération de numéros. L’arbre va générer toutes les combinaisons de “chiffres” possibles selon une stratégie donnée. Une combinaison forme ce qu’on appelle un numéro. Ensuite, on fait une association entre un numéro et une forme par l’intermédiaire de tables ou d’une fonction de conversion (un décodeur) permettant de construire la scène. Tout ceci constitue un codage de la construction d’une forme par un numéro à base n (n correspondant au nombre de couples possibles).

Une présentation et une analyse plus approfondie des arbres d’énumération sont effectuées en Annexe 4.

4.13.2 Exemple

[Elk89] et [Paj94b] utilisent la technique d’arbre d’énumération sans répétitions pour générer des configurations de segments de droite dans un plan. Chaque segment de droite que l’on peut dessiner sur une grille reçoit un numéro d’ordre. Ce numéro d’ordre sera un chiffre pour l’arbre d’énumération.

Le passage entre un chiffre et un segment se fait à l’aide :

· d’une table de conversion ;

· d’une fonction ;

· d’un algorithme spécifique.

4.13.3 Remarques

Ces arbres sont intéressants dans un univers discret et fini (parfois artificiellement en limitant la profondeur de l’arbre), où l’on peut trouver un codage performant en fonction des objets de base, de leurs caractéristiques, des opérations élémentaires et aussi des propriétés demandées. Il est possible alors d’effectuer une énumération totale de l’univers des formes solutions.

[Pas90] fait remarquer que les arbres d’énumération ont une caractéristique intéressante : certaines propriétés peuvent être vérifiées directement sur le nombre. En effet avec ces propriétés, il n’est pas nécessaire de construire la forme pour la vérifier. La connaissance du nombre et de certaines propriétés du codage permettent la vérification directement sur le nombre généré. Ainsi, il est possible “d’économiser” des constructions de formes.

Par contre, il souligne deux problèmes qui peuvent arriver pour certains codages :

· des combinaisons de chiffres peuvent être interdites (le nombre ne permet pas de construire une forme),

· des nombres différents peuvent générer une même forme.

Il est donc important de bien étudier le codage afin d’éviter qu’il y ait des combinaisons interdites et de ne générer que des formes différentes.

Toutes les techniques d’optimisation telles que l’élagage, la réduction des contrôles, la mise en place de gardes et les techniques de vérification que nous avons étudiées jusqu’ici sont bien entendu utilisables (et à utiliser !).

Le codage permet de garder une trace de la conception de la forme. Ceci est utile pour la visualisation d’une part et pour la génération du mode opératoire pour construire réellement la forme (Nous verrons cela dans un prochain chapitre).

4.14. Conclusion

L’arbre d’exploration semble une technique plus performante que l’arbre de déduction (que nous allons étudier maintenant) dans les conditions d’emploi (cf. [Mar90]) c’est-à-dire pour un univers discret et fini. En effet, toute la gestion des règles est évitée et la maîtrise de l’ordre de parcours est meilleure et plus facile. Dans certains cas, il est possible d’éviter les solutions identiques et de mettre en place un arbre d’énumération permettant de générer encore moins de mauvaises solutions (moins de formes générées, des élagages et des Réductions des contrôles plus performants).

Pour l’instant, aucune structure de données spécifique n’est utilisée pour les arbres d’exploration. Ceci est la conséquence du fait que les applications ne manipulent pas des scènes complexes.

Les arbres d’exploration posent un problème à l’implémentation. La structure idéale dans un parcours d’arbre est la récursivité. Cependant, l’appel récursif demande une sauvegarde de contexte qui peut devenir très coûteuse dans certaines applications. En effet, la structure de données est parfois très importante (par exemple avec les matrices de voxels) et les arbres très profonds. Normalement, à chaque fois qu’on descend vers un fils, il faut sauvegarder le contexte afin de pouvoir gérer le retour arrière (gestion implicite pour les appels récursifs). Il arrive très vite que la mémoire soit saturée. Pour éviter ce problème, il faut alors se contenter d’enregistrer l’action effectuée au nœud (le couple Opération-élément de base), souvent à l’aide d’une pile. Lors d’un retour arrière, l’action effectuée sera annulée. Cela implique que l’univers manipulé possède, pour chaque opération, une opération inverse qui permette de retrouver la forme de départ. A ce niveau, l’algorithme risque d’être ralenti.

Nous allons maintenant étudier une autre technique de génération : les arbres de construction.

5. Arbres de construction

5.1. Introduction

Dans tous les cas, il est possible d’effectuer la recherche des formes solutions à l’aide d’un arbre de construction appelé aussi arbre de déduction. Il est basé sur l’utilisation d’un ensemble de faits et de règles. Cette technique a été étudiée par [Bea89], [Col90], [Mar90] et surtout par [MaM89-94] et [Ple91]. Pour une synthèse sur les grandes idées des arbres de construction, on peut consulter en particulier [MaM94] et [DeM97].

Les propriétés (et donc les descripteurs) et les méthodes de construction sont décrites à l’aide de règles et de faits. Les formes sont obtenues par application des règles sur les faits.

Le mécanisme de déduction le mieux adapté semble être un moteur d’inférence d’ordre 2 fonctionnant en chaînage avant, arrière ou mixte (chaînage avant ou arrière) par tentatives, monotone, avec l’hypothèse d’un mode ouvert (cf. [MaM89-94] et [Ple91]).

Selon [Bea89], la génération doit être exhaustive (par un moteur d’inférence adapté), indépendante du modèle géométrique (à l’aide des règles), évolutive et prendre en compte la notion de multi-description (règles spécifiques de déformation).

Nous allons d’abord décrire, à travers le travail de [MaM89-94] et [Ple91], les faits et leur organisation.

Ensuite, nous verrons les règles et le moteur d’inférence pour traiter des descriptions simples, ceci permettant la description du traitement de propriétés diverses.

Enfin, nous regarderons, à travers le travail de [Bea89] et [Ple91], le traitement de descriptions complexes par des règles hiérarchisées.

5.2. Faits

Selon [MaM94], pour une scène donnée, il y a deux types de fait :

1. Les faits géométriques. Il s’agit de la représentation géométrique de la scène.

2. Les faits abstraits liés au modèle déclaratif. Ils décrivent d’une manière plus abstraite la scène étudiée. Ils peuvent correspondre à plusieurs formes terminales possibles (plusieurs modèles géométriques).

Les faits géométriques sont organisés selon un principe orienté objet. Ils sont de deux types :

1. Type complexe (possède des fils),

2. Type terminal (renferme une valeur quelconque).

[Ple91] (repris par [MaM94]) propose comme modèle géométrique (ici un modèle intermédiaire ou plutôt un modèle sur la géométrie pouvant être converti en un modèle géométrique standard comme le modèle à facettes, la représentation par les bords...) un modèle fortement hiérarchisé. Il reprend les notions de description par décomposition hiérarchique ou par composition. Il calque cette description à la structure de données. Chaque objet de la scène peut être composé d’un ensemble d’objets plus simples. Cette hiérarchisation (arborescence) peut être utilisée aussi pour l’étude des propriétés en mettant en place les notions de composition, de généralisation, de spécification, d’héritage des propriétés mais aussi de niveau de détail.

La nature des faits dépend souvent du type de la scène, de la méthode de modélisation ou de la méthode de génération choisie. Généralement, il propose de ne créer qu’un seul fait qui sera modifié pendant la génération.

Au départ, il comporte :

· l’emplacement d’un point particulier de l’espace de travail constitué par la boîte englobante de la scène,

· les dimensions de cet espace de travail,

· des renseignements supplémentaires dépendant du type de description et contenant la discrétisation de l’espace de travail...

Dans le cas d’une description par composition d’objets, il propose autant de faits que d’objets utilisés pour la scène.

A partir du modèle externe (description de l’utilisateur), il faut définir les règles de déduction (modèle déclaratif). Les propriétés et les objets de la scène sont représentés par des règles.

5.3. Règles pour des scènes simples

Nous allons supposer ici, que l’utilisateur propose une description simple. Les règles sont alors organisées par rapport à leur rôle et non pas par rapport à une hiérarchisation imposée par la description.

[MaM94] propose de classer les règles en 7 classes :

1. Les règles de construction. Elles permettent de produire des faits nouveaux dans la base de connaissance. Elles sont chargées des calculs d’entités géométriques à partir d’autres, ou de produire des connaissances plus abstraites à partir de déductions logiques. Elles font appel à une procédure de calcul spécifique pour assurer une certaine efficacité dans la déduction.

2. Les règles de modification. Elles permettent de changer la valeur d’un fait sans remettre en cause son existence. Elles sont adaptées au calcul de faits par approximations successives. Dans ces règles, on peut mettre en évidence deux “sous-classes” : les règles de déformation (déformation de la forme nécessaire selon [Bea89] pour traiter la multi-description) et les règles de placement (situation de la forme). (Voir [Bea89], [MaM90-91]).

3. Les règles d’évaluation. Elles permettent de donner une mesure sur une propriété particulière. Elles constituent une classe à part afin d’intégrer au moteur un traitement spécifique pour ces règles. Les faits produits par ces règles servent essentiellement aux règles de modification, pour leur donner une indication sur le degré d’obtention d’une propriété (pourcentage). D’autres règles peuvent utiliser ces faits.

4. Les règles de création. Elles permettent de créer des faits nouveaux sans avoir à calculer leur valeur en fonction des prémisses. Elles permettent par exemple la construction d’un modèle géométrique abstrait de la scène.

5. Les règles de suppléance. Elles permettent l’exploration de toutes les possibilités de valeurs d’un paramètre d’un fait terminal. Elles contrôlent l’ordre de production de ces valeurs et l’échantillonnage. Ce sont ces règles qui sont responsables de la construction de l’arbre. Elles utilisent des techniques de résolution de contraintes. Elles posent le problème de l’exploitation d’un ou plusieurs intervalles (discrétisation...) par résolution de contraintes et tirages de valeurs dans un intervalle (tirages aléatoires, aléatoires sous contrôle, réguliers...)

6. Les règles de vérification. Elles déterminent si une propriété est vérifiée ou non. Elles permettent un contrôle a posteriori des objets produits et la mise en place d’élagages.

7. Les règles de contrainte. Elles permettent d’exprimer des relations entre les différents faits sous forme de systèmes d’équations et d’inéquations. Elles permettent de réduire les intervalles de définition de certains faits.

Pour une propriété, les règles de vérification peuvent être implémentées de deux manières :

1. par une seule règle faisant appel à une procédure spécifique,

2. par un ensemble de règles qui vont être traitées par un moteur en chaînage arrière.

[Col90] propose aussi un classement des règles en 5 types :

1. Les règles d’optimisation de parcours. Elles permettent d’optimiser l’étude de l’arbre de construction en opérant des élagages irréversibles. Ces règles sont basées sur les propriétés des formes.

2. Les règles constructives. Elles dirigent la construction des formes en déterminant quels sont les fils intéressants des nœuds des arbres. Elles conduisent à des formes possédant automatiquement une propriété donnée et donc à étudier des formes qui ont plus de chance de répondre à la description. Seulement, elles risquent de générer un arbre non fiable.

3. Les règles destructives. Elles indiquent les opérations qu’il vaut mieux éviter de faire sous peine de ne pas obtenir, de façon définitive, une propriété. Elles éliminent le maximum de situations défavorables et irréversibles. Elles ne posent pas les problèmes de non-fiabilité des règles constructives.

4. Les règles directives. Elles consistent à orienter l’ordre dans lequel les opérations sont effectuées. Elles regroupent les formes solutions dans l’arbre de sorte que les optimisations de parcours, élagages et réductions des contrôles puissent être appliqués plus avantageusement.

5. Les méta-règles. Elles manipulent les règles en les ajoutant, en les enlevant ou en les modifiant.

Afin d’optimiser l’étude des propriétés sur les formes partielles, [Col90] propose aussi une classification de règles permettant de suivre l’évolution des propriétés sur ces formes :

· Les règles de conservation. Elles indiquent si les propriétés de la forme partielle sont conservées lors de l’application d’une ou plusieurs actions élémentaires, lors de la construction du fils d’un nœud.

· Les règles de modification. Elles permettent de modifier une propriété lors de l’application d’une ou plusieurs actions élémentaires sur la forme partielle. La forme possède une propriété qui sera différente après l’application d’une ou plusieurs actions élémentaires.

· Les règles de suppression. Elles font disparaître les propriétés qui ne sont plus vérifiées après une action élémentaire. Elles permettent de mémoriser d’anciennes propriétés qui sont susceptibles de réapparaître.

· Les règles d’apparition. Elles permettent de déterminer de nouvelles propriétés ou de retrouver des propriétés disparues des formes partielles. Elles sont de trois catégories : celles qui amorcent le processus de gestion des propriétés, celles qui détectent des propriétés disparues à partir d’informations mémorisées et celles qui découvrent de nouvelles propriétés.

Comme les propriétés, ces règles peuvent être gardées c’est-à-dire qu’il est possible de mettre en place une garde à chaque règle permettant de signaler si la règle concernée peut être étudiée. Une garde est alors considérée comme une méta-règle puisqu’elle permet de déterminer si une règle, associée à une propriété, peut ou non être applicable.

Remarque : Comme on associe à une propriété plusieurs règles, celles-ci vont pouvoir être de 4 types : suffisantes, nécessaires, non fiables ou incorrectes.

[MaM94] souligne que le choix d’une règle à appliquer doit se faire suivant un ordre précis :

1° Les règles d’évaluation ;

2° Les règles de modification ;

3° Les règles de contraintes ;

4° Les règles de vérification ;

5° Les règles de construction ;

6° Les règles de création ;

7° Les règles de suppléance.

Plus récemment [MaM96] propose une nouvelle classification des règles (par ordre d’application) :

1. Les règles de calcul. Ces règles correspondent à un calcul procédural traditionnel.

2. Les règles de contraintes. Elles réduisent un ensemble d’intervalles des faits à l’aide de l’arithmétique d’intervalles.

3. Les règles de suppléance. Elles permettent l’exploration des différentes possibilités de scènes répondant à une description.

4. Les règles de vérification. Elles effectuent un contrôle a posteriori sur la validité des valeurs qui sont produites.

5.4. Fonctionnement d’un moteur d’inférences pour des scènes simples

[MaM94] proposent un moteur d’inférence fonctionnant en chaînage avant. Une forme solution est obtenue à la saturation de la base (plus aucune règle n’est applicable). Nous verrons que cette solution se rapproche de la démarche constructive pour des descriptions complexes.

Une règle applicable est une règle dont les prémisses peuvent s’unifier à des faits connus de la base.

Une règle productive est une règle qui en s’appliquant produit quelque chose de nouveau. L’application de cette règle provoque l’apparition d’un fait nouveau qui peut ensuite être ajouté à la base de connaissances.

Pour choisir la prochaine règle à appliquer, on prend une règle productive dans le premier groupe (dans l’ordre défini dans le paragraphe précédent), non vide et possédant des règles productives. Le choix de la règle à l’intérieur du groupe et des faits en prémisses (problèmes d’unification) ne dépend que des problèmes d’optimisation liés au domaine.

Pour optimiser le traitement des règles, plusieurs solutions du même ordre ont été proposées : instaurer des niveaux de déclenchement et de suppression. Une règle n’est alors utilisable que dans certaines conditions spécifiques de la base de connaissances.

[MaM89] propose de séparer le traitement en niveaux, chacun regroupant un certain nombre de règles de même famille. Le passage au niveau suivant se fait seulement après saturation du niveau courant. La forme complète n’est obtenue qu’après saturation du dernier niveau. Par exemple, il propose trois niveaux : les règles 2D, 3D et les règles de visualisation.

Cependant, cette séparation n’apparaît plus explicitement dans [MaM96]. Cependant, ils gardent la notion de groupe (1 pour les règles de vérification, 2 pour les règles de calcul et de contrainte et 3 pour les règles de suppléance). L’algorithme consiste à appliquer prioritairement les règles de groupe de numéro le plus faible. Leur moteur fonctionne selon le principe suivant :

1. les règles de vérification valident les faits existants (elles sont appliquées en priorité) ;

2. les règles de calcul et de contraintes (dites règles de réduction) sont appliquées tant que c’est possible ;

3. les règles de suppléance effectuent des choix afin de relancer les étapes précédentes (elles sont appliquées en si les deux étapes précédentes ne peuvent pas l’être) ;

4. La scène est construite lorsque plus aucune règle n’est applicable et que les règles de vérification sont toutes valides.

5.5. Règles pour des scènes complexes

5.5.1 Introduction

Nous supposerons, ici, que l’utilisateur fait une description structurée (par exemple d’une manière hiérarchique). Donc, les règles seront organisées en conséquence.

[Ple91] propose deux solutions pour représenter les règles :

1. les grammaires à attributs ;

2. les règles de type PROLOG.

5.5.2 Grammaires à attributs

Dans ce type de représentation, les règles sont définies par une grammaire à attributs. Cette grammaire est composée de la façon suivante :

· L’axiome est l’ensemble des scènes à obtenir.

· Les symboles non terminaux sont les éléments obtenus par composition ou décomposition.

· Les symboles terminaux sont d’une part les éléments non décomposés au niveau actuel de description ou les éléments de base à composer et d’autre part les opérateurs.

· Les attributs permettent de définir les contraintes de forme des objets au niveau de chaque règle.

· Les règles de la grammaire rendent compte de la décomposition des objets ou de la façon de les composer. Associées aux attributs, elles permettent la déduction des propriétés d’héritage et de synthèse.

Le problème de cette représentation est le suivant : l’ensemble des opérateurs est figé et difficilement extensible. Pour cela, entre autres, on préférera la représentation par des règles de type PROLOG.

5.5.3 Règles PROLOG

Les règles sont représentées par un ensemble de règles de déduction de type PROLOG. Cette représentation permet une facilité d’extension du modèle par ajout d’autres possibilités de description (écriture de nouvelles règles).

Remarque : [Dje91] utilise directement le moteur de Prolog pour effectuer sa génération mais ne donne pas de détails sur les règles utilisées.

De manière générale, les règles sont composées de la façon suivante :

· La conclusion est la partie courante de la scène à engendrer (en fonction de son niveau dans l’arbre de description). C’est le nom de la scène à décrire.

· Les prémisses expriment les contraintes spatiales entre les éléments, les contraintes de taille et les propriétés de haut niveau décrivant la forme.

Pour les descriptions comportant des alternatives, plusieurs règles de même conclusion seront générées, chaque règle décrivant une alternative.

Il faut noter qu’un cas n’est pas facile à traiter avec ce système (organisation hiérarchique) : c’est la gestion d’un nombre approximatif de sous-scènes dans une scène donnée.

Finalement, [Ple91] montre que le moteur d’inférence de PROLOG n’est pas adapté pour la génération de formes en modélisation déclarative (entre autres, prise en compte des contraintes, fonctionnement en chaînage avant, environnement de programmation pauvre, calculs lourds, performances médiocres...).

[Ple91] et [MaM94] proposent d’autres moteurs plus adaptés (celui de [Ple91] semble beaucoup moins général que celui de [MaM94] du fait de sa gestion de descriptions très structurées). Ils ont, entre autres, les avantages d’être adaptés au mode de génération choisi, d’être plus pratiques pour les calculs numériques et plus performants. Par contre, le concepteur doit écrire le moteur et implémenter tous les mécanismes qui s’y rattachent (d’où l’utilité d’un noyau le plus souple possible). Le système est alors un peu lourd et rigide pour l’ajout de nouvelles règles.

5.5.4 Classement des règles

[Bea89] distingue trois grands types de règle :

· Les règles de type 1. Ce sont les règles associées aux descripteurs géométriques, de relations spatiales et de décomposition. Elles permettent la construction d’une surface médiane (sorte de squelette épais) déterminant les intervalles des paramètres pour les règles de déformation.

· Les règles de type 2. Ce sont les règles associées aux descripteurs de formes (globaux ou locaux), à un coefficient de déformation (traduit l’importance de la propriété dans la forme) et à un rayon d’action (limite la portée de la propriété sur la forme, localise plus ou moins la propriété).

· Les règles classiques. Ce sont les règles spécifiques au modèle géométrique, les règles de composition et les règles d’héritage.

[Ple91], pour son organisation hiérarchique des règles, prend en compte trois types de règle :

1. Les règles non terminales constructives. Ces règles servent à indiquer la décomposition hiérarchique de la scène à engendrer. Elles sont générées à partir de la description. Elles sont appliquées jusqu’à saturation.

2. Les règles non terminales non constructives. Elles ne sont appliquées qu’une seule fois.

3. Les règles terminales. Elles indiquent des propriétés ou des éléments de la scène. Leur définition est faite par ailleurs soit de façon impérative soit sous forme d’un ensemble de règles pré-définies. Elles ne sont appliquées qu’une seule fois.

5.5.5 Ordre d’application des règles

[Bea89] propose 11 principes permettant de déterminer un ordre d’application des règles en ce qui concerne la notion de déformation :

1- Les règles du type 1 doivent être appliquées avant celles de type 2 pour que les propriétés associées soient prises en compte lors de la génération.

2- Soient trois primitives de forme distinctes P1, P2, P3. Appliquer à une entité donnée ces trois primitives dans l’ordre P1, P2, P3 n’est pas équivalent à l’ordre d’application P2, P3, P1...

3- L’importance relative d’une propriété de type 2 sera d’autant plus grande que la règle associée sera appliquée le plus tard possible.

4- Les règles de type 2 associées aux propriétés les plus importantes doivent être appliquées après les autres règles. Cela amène à classer les règles par importance équivalente.

5- La forme de l’entité initiale n’intervient pas sur la forme finale obtenue si on applique chaque règle associée à une zone de l’entité considérée (ou l’entité globale) avec un coefficient de déformation de 100%.

6- Pour deux classes de règles de type 2, C1 et C2 telle que C1 contient des propriétés plus importantes que celles de C2, augmenter de quelques points le coefficient de déformation de la classe C1 par rapport à celui de C2 ne remet pas en cause le principe 3.

7- De même, à l’intérieur d’une même classe, on peut modifier les coefficients de déformation de chaque règle de type 2, ce qui induit un ordre total dans cette classe.

8- Une règle de type 2 peut être appliquée plusieurs fois sur la même entité, ce qui aura pour effet de faire converger la forme résultante vers cette primitive de forme.

9- L’importance relative d’une propriété de type 1 sera d’autant plus grande que la règle associée sera appliquée le plus tôt possible.

10-Les règles du type 1 associées aux propriétés les plus importantes doivent être appliquées avant les autres règles.

11-Une condition nécessaire pour que les principes énoncés précédemment restent valides est que, pour une entité donnée, toutes les primitives de forme qui lui sont appliquées (règles de type 2) aient une taille équivalente.

Pour [Ple91], l’ordre des règles est régi par l’ordre des prémisses. En effet, les règles sont hiérarchisées par la description. Au départ, il n’existe qu’un seul fait. Seules les règles ayant pour conclusion la scène globale peuvent être prises. Comme elles sont utilisées en chaînage arrière, les règles seront appliquées selon l’ordre des prémisses.

Afin d’optimiser la génération (plus particulièrement, pour limiter le nombre de solutions à générer) [Ple91] propose de réorganiser les prémisses, juste avant la génération, de manière à produire le moins de formes possibles.

Lors de l’application d’une règle, il propose l’ordre suivant :

1. règles de dimensions ;

2. règles de décomposition ;

3. règles de taille ;

4. règles de placement ;

5. règles de forme.

Pour [Ple91], une règle applicable est une règle dont la conclusion coïncide (est unifiable) avec le fait à établir et n’est pas saturée par rapport à la discrétisation de l’espace.

5.5.6 Héritage et synthèse

Les notions d’héritage et de synthèse sont présentées par [Ple91] autour de la notion de description hiérarchique. Certaines propriétés sont héritables, d’autres pas ou pas totalement. D’autres le sont seulement selon le type de décomposition, le type d’application... Seules quelques propriétés peuvent être héritées ou synthétisées indépendamment de toute autre considération. Il convient de bien déterminer les caractéristiques de chacune à ce niveau. Ces techniques (en plus des contraintes de placement et de taille), permettent d’optimiser le parcours de l’arbre de déduction en provoquant certains élagages (particulièrement grâce aux propriétés d’héritage).

L’héritage est le fait, pour une propriété donnée de se répercuter dans les règles décrivant les sous-scènes d’une scène courante. La propriété est alors prise en compte par les sous-propriétés. L’héritage s’utilise, par exemple, pour gérer les propriétés globales qui doivent être répercutées sur toutes les sous-scènes d’une scène donnée.

La synthèse consiste à prendre en compte certaines propriétés des sous-scènes pour traiter la scène courante. Nous verrons, dans le chapitre traitant de la visualisation des solutions que le calcul d’un bon point de vue peut être effectué en fonction des bons points de vue des sous-scènes et des caractéristiques de la scène courante. Ceci est un exemple de synthèse.

5.6. Fonctionnement d’un moteur d’inférences pour des scènes complexes

5.6.1 Principes

[Ple91] propose des solutions spécifiques adaptées à la structuration hiérarchique. Le système de génération doit pouvoir gérer :

· la loi de génération (approche constructive, d’où un moteur en chaînage avant) ;

· les contraintes (approche destructive, d’où un moteur en chaînage arrière).

La génération peut être considérée de deux points de vue différents :

1. La génération ascendante. C’est une méthode de génération par addition ou composition. Elle opère par assemblage d’objets de base, addition de matière. La modélisation par composition en est un exemple.

2. La génération descendante. C’est une méthode de génération par soustraction ou décomposition. On part d’une approximation grossière (boîte englobante) puis on affine progressivement pour obtenir un ensemble de scènes. On opère un raffinement progressif par suppression de matière. La modélisation par décomposition hiérarchique fait partie de cette catégorie.

Il existe deux démarches possibles :

1. La démarche constructive-destructive. Les règles de contrainte sont traitées différemment des autres règles. Cette solution est cohérente mais nécessite un moteur fonctionnant en chaînage mixte.

2. La démarche constructive. Un moteur classique avant ou arrière est utilisé avec des règles qui décrivent l’influence des contraintes sur les objets. Cette solution est plus générale mais est plutôt lourde et demande un nombre important de règles.

Remarque : le système est nécessairement orienté vers le type d’objets qu’il est supposé engendrer. En effet, il faut, d’une part faire certaines hypothèses sur la représentation interne des objets et d’autre part, choisir parmi des fonctions prédéfinies. Malgré tout, il semble possible d’extraire un noyau commun et un certain nombre de généralités.

5.6.2 Démarche constructive-destructive

Pour cette démarche, le moteur d’inférences doit fonctionner en chaînage mixte (avant et arrière). Deux stratégies sont possibles :

1. Le moteur ne traite, dans un premier temps, que les règles de génération en chaînage avant. La résolution des règles de contraintes n’intervient qu’à l’issue de l’obtention d’une solution par l’application des seules règles de génération sur les objets obtenus (par chaînage arrière). Ce système a l’avantage de séparer les règles de construction (loi de génération) des règles de contraintes. Cependant ce système est lourd car toutes les solutions sont générées avant d’être vérifiées et la séparation des deux types de règles n’est pas toujours possible. Cette stratégie correspond à une génération systématique des formes.

2. Les règles de contraintes interviennent à partir du niveau le plus bas de l’arbre de construction, elles sont appelées au fur et à mesure de la construction. Cette solution est plus économique que la précédente car on voit moins de formes.

Il existe plusieurs solutions pour l’architecture d’un tel système, dont les deux suivantes :

1. Un moteur unique pouvant travailler dans les deux sens selon le cas.

2. Deux moteurs (un en chaînage avant pour les règles de génération et un en chaînage arrière pour les contraintes) sont sous la dépendance d’un moteur “maître”. Ce dernier répartit les règles entre les deux autres et gère les bases de faits associées (les deux moteurs peuvent fonctionner en parallèle). Il lit les règles en commençant par celles dont la conclusion est le fait à établir. Selon que les prémisses sont constructives, destructives ou des deux types, il envoie la règle respectivement au moteur avant, arrière ou aux deux. Chaque moteur possède sa base de faits. Le moteur avant travaille sur une base de faits initiaux et les faits nouveaux sont placés dans la base du moteur arrière. Le moteur arrière possède sa base propre et les faits nouveaux sont placés dans la base de faits initiaux.

Cette démarche semble, selon [Ple91], adaptée pour la modélisation par composition. Nous avons alors affaire à une construction ascendante.

5.6.3 Démarche constructive

Pour ce cas, toutes les règles sont constructives (un seul type de règle). On est sûr que les objets construits respectent les contraintes. Il faut donc utiliser un moteur classique en chaînage avant ou arrière travaillant sur les objets de la base.

La démarche constructive semble adaptée pour la modélisation par décomposition hiérarchique. Nous avons alors affaire à une construction descendante, donc un moteur fonctionnant en chaînage arrière est préférable. Cette méthode est, nous l’avons vue, très lourde (fonctionnement et nombre de solutions). [Tam95] propose quelques optimisations au niveau de la gestion des contraintes et du fonctionnement interne du moteur.

5.6.4 Remarque sur l’application d’une règle

Afin d’optimiser le traitement en améliorant l’élagage de l’arbre de construction lors d’une démarche constructive, [Ple91] propose un fonctionnement particulier du moteur arrière. Il propose de distinguer deux phases dans l’application des règles :

1- traitement des règles terminales,

2- règles appliquées normalement.

5.7. Remarque sur les arbres de construction

Comme pour les arbres de génération, l’implémentation des arbres de construction pose certains problèmes techniques. Pour chaque application de règle, il est nécessaire d’enregistrer les différents contextes (pour les retours arrières). Cela pose des problèmes au niveau de la gestion de la mémoire. Cette difficulté est accentuée par l’utilisation des arbres de composition ou de décomposition. En effet, il est clair que ces arbres impliquent une redondance d’informations et, donc, un coût supplémentaire en place mémoire.

6. Conclusion

Nous avons étudié 4 techniques de génération de scènes correspondant à une description :

1. les algorithmes spécifiques ;

2. les algorithmes basés sur un résolveur de contraintes ;

3. les arbres d’exploration ;

4. les arbres de déduction.

Les deux dernières techniques ont la particularité de pouvoir produire toutes les formes solutions lorsque l’univers dans lequel ils travaillent est fini.

Les algorithmes peuvent être répartis entre deux modes naturels de génération (Cf. [Paj94b]) :

1. Le mode exploration. Ce mode comprend les algorithmes qui permettent une énumération totale de toutes les solutions possibles vérifiant une description donnée. Il est utilisé pour des univers énumérables. Les algorithmes types sont les arbres d’exploration et de construction lorsque l’univers dans lequel ils travaillent est fini. C’est le mode idéal pour un système déclaratif.

2. Le mode échantillonnage. Ce mode fait référence aux algorithmes qui ne vont donner qu’une ou plusieurs solutions vérifiant la description. Toutes les solutions ne seront ou ne pourront pas être atteintes. L’algorithme type est le tirage aléatoire sous contrôle. En fait, ce mode peut être adopté par l’ensemble des algorithmes. Il est souvent adopté pour des propriétés portant sur des intervalles continus (comme l’utilise [Pou94b]).

Dans la suite de ce travail, et plus précisément dans la partie III (chapitre III.2), nous préférerons cette classification à celle basée sur les types d’algorithmes.

Nous allons maintenant nous intéresser à la troisième phase importante des modeleurs déclaratifs : le prise de connaissance.

Chapitre I.4
Prise de connaissance des solutions

1. Introduction

L’objectif est d’utiliser des outils pour que l’utilisateur puisse prendre connaissance des formes solutions et choisir celle qu’il préférera. C’est la phase de prise de connaissance des modèles géométriques vérifiant la description de l’utilisateur.

[Pou94b] souligne que cette prise de connaissance des solutions à la description se déroule en deux phases : d’abord l’utilisateur opère une recherche en visualisation rapide et, seulement après, la solution trouvée est observée grâce à une technique de visualisation réaliste.

[Ple91] et [Pou94b] font remarquer que la démarche déclarative est utile à la visualisation. En effet, à partir des propriétés de départ et des propriétés déduites lors de la génération, il est possible d’en déduire des propriétés utiles pour la visualisation.

Certains paramètres visuels peuvent être définis de façon déclarative et calculés automatiquement (cf. le vocabulaire concernant les caractéristiques visuelles) comme par exemple :

· l’aspect de la surface extérieure des objets de la scène à visualiser ;

· la distance et l’emplacement du point de vue (très important pour montrer le maximum de caractéristiques) ;

· l’emplacement et la nature de la ou des sources lumineuses ;

· le type d’algorithme de visualisation à choisir en fonction des propriétés particulières de la scène à visualiser.

En phase de prise de connaissance, nous trouvons plusieurs classes d’outils (Figure 7). Il existe un ensemble d’outils permettant d’explorer l’ensemble des solutions (section 3). L’utilisateur explore cet ensemble en spécifiant un ordre particulier, en filtrant certaines solutions ou par retouche contrôlée. Pour chaque solution, l’utilisateur dispose d’outils permettant de bien l’appréhender (section 4). Finalement, lorsqu’elle lui plaît, il peut obtenir un mode opératoire permettant de refaire cette solution (section 5).

Remarque : L’ensemble des solutions n’est pas toujours connu entièrement au moment de la prise de connaissance. Ces outils ne sont donc pas toujours exploitables à moins que le module de calcul puisse s’adapter dynamiquement en fonction des demandes de la phase de prise de connaissance.

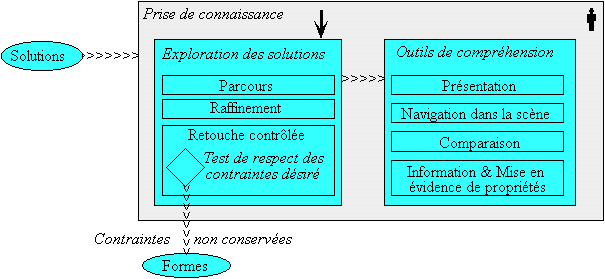
Figure 7. La phase de prise de connaissance [CDMM97]

2. Génération et prise de connaissance

Il existe trois possibilités pour montrer une forme solution à l’utilisateur :

1. La visualisation se fait au cours de la recherche des solutions. Dès qu’une forme solution (forme complète) est trouvée, elle est proposée à l’utilisateur. C’est la démarche retenue par [MaM89-94] par exemple.

2. La visualisation se fait une fois que toutes les solutions ont été trouvées, après la phase de recherche des solutions. Chaque solution est mise de côté. La phase de visualisation est alors complètement indépendante de la phase de recherche des solutions.

3. L’exploration est guidée par l’utilisateur. La visualisation se fait au fur et à mesure du traitement. Non seulement les formes complètes sont visualisées pendant le traitement mais les formes partielles le sont aussi.

La première possibilité risque de présenter plusieurs fois la même forme solution (sauf, évidemment, pour les arbres d’énumération). De plus, l’ensemble des solutions est plus difficile à manipuler. La seconde pose un problème pratique important : en effet, souvent le nombre de solutions est tel qu’il n’est pas possible de tout stocker.

3. Exploration des solutions

3.1. Parcours des solutions

Si plusieurs formes sont solutions de la description, le problème est de déterminer l’enchaînement des formes à visualiser.

[MaM94] propose un certain nombre de points importants qui doivent être traités dans ce type d’application :

· ne pas proposer toujours les mêmes formes dans le même ordre (La prochaine forme sera calculée différemment, certains facteurs étant tirés aléatoirement comme le choix d’une règle, l’ordre des valeurs prises dans un intervalle...) ;

· pouvoir, au contraire, retrouver facilement une forme déjà vue (triées selon un ordre bien déterminé) ;

· montrer des formes les plus variées possibles parmi les solutions potentielles ;

· présenter une bonne interactivité afin que l’utilisateur puisse garder le contrôle de l’exploration.

Dans le cas des techniques de tirage aléatoire, ce problème ne se pose pas. Même si plusieurs solutions peuvent être présentées, aucun contrôle n’est faisable. Plus généralement, c’est le cas pour toutes les techniques en mode échantillonnage n’utilisant pas les arbres de génération.

Pour un petit nombre de solutions, il est envisageable de faire une visualisation systématique ([Col90a-b]), c’est-à-dire de consulter toutes les solutions. L’affichage peut se faire selon différents ordres : l’ordre de génération, l’ordre de stockage (qui peut être le même que l’ordre de génération) ou selon certains critères comme la proximité de telle ou telle propriété...

Lorsque les solutions sont stockées, il est alors possible de réaliser, d’une manière ou d’une autre un tri selon les critères choisis.

Une solution possible ([Col90]) est de ne pas commencer toujours par la même solution. Selon la stratégie considérée par l’utilisateur, la forme initiale est alors :

· La dernière forme affichée. La visualisation se poursuit à l’endroit même où celle-ci s’est arrêtée lors de la dernière séance de travail.

· Une forme tirée au “hasard contrôlé”. L’utilisateur désire observer des formes qui se suivent dans un ordre fixé à partir de l’une d’elles. Il peut choisir une forme déjà vue ou provenant d’une nouvelle région, à un point de départ fourni aléatoirement.

· La première forme engendrée. On suppose alors que les formes sont construites dans un ordre déterminé et dans le sens des désirs de l’utilisateur (les formes les plus intéressantes sont créées en premier).

Lorsque la génération est effectuée par un arbre d’énumération ([Paj94b] et [Pou94b]), il est possible d’ajouter la situation suivante : la forme ayant un numéro donné dans l’arbre.

Une piste possible pour rechercher la bonne solution est de se rendre compte que, d’une certaine manière, les solutions sont triées car elles sont données dans l’ordre de parcours de l’arbre (souvent un parcours préfixé c’est à dire, le noeud puis les fils). Ceci est particulièrement vrai si la technique de génération est l’arbre d’énumération. L’étude des formes solutions revient alors à choisir une stratégie de parcours de cet ensemble ordonné de solutions. Il est même alors possible de faire des retours en arrière sur des solutions déjà vues même si la visualisation se fait pendant la génération.

Mais le nombre de solutions peut être très important, voire infini. L’exploration de ce grand nombre de solutions (cf. [LMM89]) pose alors un problème. Il sera donc intéressant de pouvoir raffiner cet ensemble de solutions.

3.2. Raffinement des solutions

Il faut donc ne plus vouloir voir toutes les solutions mais effectuer un échantillonnage selon différentes stratégies. Il y a alors un raffinement des solutions.

[Col90a-b] propose une visualisation partielle des formes. En effet, compte tenu du nombre de solutions, il n’est plus envisageable de toutes les visualiser. Il apparaît alors nécessaire de proposer quelques outils afin de voir seulement certaines d’entre elles.

[Ple91] propose plusieurs stratégies :

· Le concepteur définit un pas P. Les scènes sont proposées toutes les P scènes.

· Le concepteur définit un pas P. Le système n’engendre qu’une scène toutes les P scènes.

· P peut être modifiable.

· Les scènes sont tirées au hasard.

· Le système définit des classes de scène en s’aidant de propriétés non demandées. Il ne propose qu’un représentant de chaque classe.

· L’utilisateur choisit un niveau de détail. Puis, il sélectionne une des solutions proposées et recommence. Le choix est affiné ainsi progressivement. C’est une exploration dirigée.

Remarque : les deux dernières solutions peuvent être combinées afin d’opérer une exploration par classement et raffinement progressif.

La notion de pas entre deux formes est reprise par [Pou94b]. Il utilise sa technique de numérotation afin de ne générer qu’une forme tous les P pas.

Une autre technique de visualisation est la visualisation avec “hasard contrôlé” ([Col90a-b]). Dans ce cas, il faut supposer que les formes ont une répartition inconnue. Le tirage des solutions à visualiser se fait d’une manière aléatoire en considérant que les solutions sont équiprobables. Un contrôle est possible en marquant les solutions déjà vues afin de pouvoir en demander une n’ayant encore jamais été observée et de pouvoir contrôler la zone dans laquelle elle sera choisie (zone proche ou éloignée de celle de la dernière forme visualisée selon les désirs de l’utilisateur).

Afin de déterminer plus efficacement la forme solution, [Col90a-b] propose deux techniques de visualisation dirigée :

1. La dichotomie interactive. Elle procède par un dialogue avec l’utilisateur. Les formes solutions sont classées selon certains critères. Un représentant de chaque classe est présenté à l’utilisateur. Celui-ci détermine les propriétés et les caractéristiques qu’il veut ou ne veut pas voir. Les formes sont à nouveau classées puis on recommence jusqu’à l’obtention d’une forme qui plaise. Cette solution implique de pouvoir comparer deux formes et surtout de calculer un coefficient de ressemblance entre les formes ([Mar90] et [Pou94b]).

2. L’exploration de l’univers des formes solutions. On considère alors que visualiser les formes solutions revient à rechercher des solutions intéressantes dans un univers fini de formes. Il semble donc intéressant d’utiliser un arbre d’exploration, ou une autre technique, pour rechercher les solutions “solutions” (!). L’utilisateur peut préciser d’autres caractéristiques que doivent respecter les formes solutions. Ainsi, par affinements successifs, l’utilisateur choisit sa solution.

Une hypothèse est de considérer que deux formes ont d’autant plus de chances d’être différentes que les valeurs de leurs paramètres sont différentes ([MaM94]). Par conséquent, pour trouver une forme radicalement différente, il serait nécessaire de trouver une forme dont les valeurs des paramètres soient très différentes de celles de la forme courante. Cette hypothèse n’est pas systématiquement vérifiée, mais il s’avère qu’elle fonctionne souvent. De même, pour trouver deux formes très semblables, il suffit qu’elles aient les valeurs de leurs paramètres très proches. Bien sûr, ceci n’est plus valable si des paramètres ont un comportement chaotique : pour deux valeurs très proches du paramètre, il est alors impossible de dire si la nouvelle forme sera ou non similaire à l’ancienne.

[Bea89] propose une solution qu’il appelle la génération dirigée. Cette solution est reprise par [Ple91]. L’utilisateur va intervenir lors de la recherche des solutions soit pour modifier la scène (apporter des modifications impératives) soit pour décider des choix de valeurs pour certains paramètres. Cette solution peut s’appeler la génération interactive.

3.3. Retouche d’une solution

Lorsque la solution sera suffisamment satisfaisante, si elle ne convient pas encore parfaitement, l’utilisateur pourra alors la retoucher soit manuellement à l’aide des outils classiques des systèmes de CAO, soit en proposant des modifications “ponctuelles” à l’aide d’un vocabulaire adapté.

3.3.1 Retouche contrôlée

La retouche contrôlée est un autre moyen d’explorer l’espace des solutions. A la vue d’une solution, l’utilisateur souhaite parfois modifier un détail, la retoucher interactivement mais tout en conservant les contraintes issues de la description. Comme l’espace des solutions contient toutes les solutions, les formes modifiées appartiennent à cet ensemble. La modification interactive d’une solution revient à rechercher et à visualiser celles qui correspondent à la retouche décrite par l’utilisateur. Il s’agit d’une exploration particulière de l’espace des solutions. La modification désirée par l’utilisateur n’est pas toujours possible en respectant la description. Dans ce cas, le modeleur l’avertit de la violation des contraintes et lui laisse la liberté d’outrepasser les spécifications. Mais, dans ce cas, le modeleur produit une forme qui n’est plus une solution. Il communique au concepteur une mesure de l’erreur commise par rapport au cahier des charges. ([CDMM97])

[Sir97] propose une méthode d’exploration des solutions s’approchant de la retouche contrôlée. En effet, son modeleur va fournir une pyramide d’ensoleillement englobant toutes les facettes possibles (appelées masques) pouvant servir de solution (pour cacher le soleil par exemple). Il propose à l’utilisateur une solution quelconque. Celui-ci déplace le masque à loisir dans la pyramide. Il peut ainsi explorer les solutions à sa guise tout en restant dans les limites de la pyramide.

3.3.2 Modification déclarative

[Paj94b] propose, pour l’application FiloTableaux (application qui permet la génération automatique de tableaux de fils) de modifier la solution proposée à l’aide d’un vocabulaire adapté : nous appellerons cela la modification déclarative. L’objectif est d’arriver à une solution satisfaisante par dialogue avec l’utilisateur. Nous avons alors besoin d’un vocabulaire de modification et non pas de description. Cela va permettre de modifier plus finement la solution obtenue. Nous retrouvons la même idée dans [Pou94a] et [Chau94]. Chaque classe de propriétés (surtout pour celle concernant les relations spatiales) comporte un vocabulaire de description et un de modification. L’exploration succédant à la modification est une exploration sur l’ensemble des solutions ou une nouvelle génération de solutions.

Remarque : La modification déclarative est une première approche qui pourrait mener à une modification interactive par une communication vocale avec la machine.

3.3.3 Remarque

Ces techniques semblent intéressantes en particulier pour les générations en mode échantillonnage. En effet, si une solution correspond pratiquement à la description, la génération d’une nouvelle solution peut donner une solution totalement différente et inintéressante. Il est alors plus intéressant de modifier la solution pour corriger les imperfections que de risquer de tout perdre. De plus, elles permettent de conserver une bonne connaissance de la forme solution dans l’objectif de la visualisation.

Bien sûr, une technique de CAO plus classique (utilisation de la souris et d’autres outils) peut être, dans le cas d’applications 2D ([Paj94b]), plus simple et surtout plus rapide. Cependant, l’utilisateur risque de sortir de l’ensemble des solutions et de perdre l’avantage du modeleur déclaratif (connaissances issues de la description et déduites de la génération). C’est pour cela qu’il faut plutôt s’intéresser à la retouche contrôlée si la modification déclarative n’est pas utile ou trop lourde à mettre en place.

4. Compréhension d’une solution

4.1. Introduction

S’il connaît parfaitement leur description, puisqu’il l’a donnée au modeleur, l’utilisateur n’en connaît pas pour autant leur aspect. Il est très difficile de manipuler, d’appréhender, avec des outils conventionnels des formes que l’on ne connaît pas. De façon générale, comme avec tout système de haut niveau, présenter une solution sans explication n’est pas suffisant. Aussi, les modeleurs déclaratifs mettent à la disposition du concepteur une panoplie d’outils de compréhension de haut niveau pour l’aider à appréhender la structure et les propriétés (demandées ou non) des solutions. ([CDMM97])

Deux classes de techniques (voir [Ker89] et [Col90]) sont possibles. Ce sont celles qui s’appliquent à :

· la scène considérée globalement, la plus classique étant la recherche d’un bon point de vue ;

· des composantes particulières de la scène comme l’utilisation d’un ou plusieurs bons modes de visualisation.

4.2. Bon point de vue

Il faut trouver une position de l’observateur telle qu’il puisse “voir” le plus possible de propriétés (et surtout les plus intéressantes) sur la forme pour l’aider à mieux l’appréhender. Cette position sera appelée une bonne vue. Ce ne sera pas forcément la meilleure (si elle existe) mais plutôt une vue convenable. Les méthodes de recherche d’un bon point de vue ont été étudiées principalement par [Char87], [Col87], [Ker89], [Col90b], [Ple91], [Dje91] et [Pou94b].

Il existe deux familles de méthodes de recherche automatique d’un bon point de vue :

1. les méthodes “a priori”,

2. les méthodes “a posteriori”.

Ces méthodes peuvent aussi s’appliquer pour la recherche d’une bonne position des sources lumineuses.

Il est important de noter que le système recherche UN bon point de vue. Nous avons donc affaire à une recherche de point de vue en mode échantillonnage et ceci, quel que soit le type de génération des formes.

4.2.1 Méthodes “a priori”

Les méthodes “a priori” utilisent, pour leur calcul, les connaissances accumulées par le système à partir de la description des propriétés. Elles utilisent les connaissances de la forme pour mettre en valeur les propriétés. Elles dépendent du type d’informations connues mais sont totalement adaptées aux systèmes déclaratifs (utilisation des connaissances déclarées ou déduites).

Les méthodes “a priori” travaillent donc sur les propriétés des formes engendrées et sur leur représentation interne de haut niveau, indépendamment du modèle géométrique choisi pour la visualisation.

Une des méthodes a priori est la méthode d’intersection des régions d’observation. Elle permet d’utiliser les informations géométriques déduites pendant la génération. Le principe est de définir un ensemble de régions d’observation de l’espace géométrique. Chacune est une région privilégiée pour une propriété donnée (symétries...). L’objectif est de trouver la région intersection de ces régions. Si elle existe, le bon point de vue se trouve à l’intérieur. Par contre, si elle est vide, il faut d’abord essayer d’agrandir les différentes régions puis tenter, à nouveau, de trouver l’intersection.

En cas de nouvel échec, on en déduit qu’il n’est pas possible de calculer une meilleure vue par cette méthode.

Cependant, il reste possible de calculer une bonne vue grâce aux deux méthodes suivantes :

1. la définition de priorité sur les propriétés,

2. la diminution du nombre de propriétés à mettre en évidence.

[Ple91] propose une technique utilisant la structure de données hiérarchique. Pour chaque scène (pour un nœud donné), le bon point de vue est calculé à partir des bons points de vue des différentes sous-scènes, des propriétés de forme et de placement du niveau courant. La combinaison des différents points de vue se fait grâce à une formule empirique prenant en compte la taille de chaque sous-scène (par les boîtes englobantes) ou forme et leurs placements relatifs (par l’utilisation des repères des sous-scènes et du repère courant). Le calcul se fait donc grâce à l’utilisation des propriétés d’héritage et de synthèse.

4.2.2 Méthodes “a posteriori”

Le système n’a aucune connaissance préalable sur les propriétés de la forme. Les méthodes “a posteriori” n’utilisent pas de connaissances déclarées ou déduites pendant la génération pour mettre en valeur les propriétés. Elles ne disposent que du modèle géométrique de représentation interne de la forme utilisée pour la visualisation.

Une des méthodes a posteriori est la méthode basée sur le poids des formes. Cette méthode consiste à prendre un certain nombre de points de vue répartis uniformément autour de la forme et équidistants. Pour chaque point de vue, la forme est évaluée.

Ensuite, deux solutions se présentent :

1. Le nombre de points de vue est important, celui ayant la meilleure évaluation est choisi.

2. Le nombre de points de vue est faible, un nouveau point est calculé en fonction des meilleurs points.

L’évaluation d’un point de vue est basée sur le calcul du poids de la forme vue de cette position. Le poids est calculé en fonction des éléments visibles (ou partiellement visibles) de la forme et des propriétés qui doivent être mises en évidence (voir [Col87] et [Col90b]).

[Char87] propose aussi quelques techniques basées sur les propriétés physiques, et en particulier mécaniques (analyse inertielle par exemple), de la forme pour donner des indications sur la localisation du bon point de vue.

[Ker89] et [Pou94b] notent que, dans le cas des triplombres et, plus particulièrement, dans le cas des matrices de voxels, est mauvais tout point de vue placé sur un axe porté par deux sommets de la matrice (sauf pour attirer l’attention sur une propriété bien particulière).

[Pou94b] propose de calculer le bon point de vue en fonction du relief de la forme (pour lui, de la matrice de voxels). Il prend les trois faces les plus intéressantes. Il fait aussi son calcul en fonction de la surface maximum prise par la projection de la forme.

Selon le modèle géométrique utilisé, [Ple91] propose plusieurs méthodes “a posteriori” :

· Pour un modèle à facettes, le calcul de l’axe portant le bon point de vue se fait en étudiant le nombre de facettes visibles aux points cardinaux de la sphère englobant la scène. Cela permet de déterminer le triangle sphérique privilégié et de l’affiner suffisamment par subdivisions.

· Pour un modèle d’arbres CSG, il propose une technique proche d’un lancer de rayon sur les trois axes principaux.

· Pour un modèle en arbres octaux, il utilise une technique proposée aussi par [Col90b] sur la quantité de cubes visibles pour une direction donnée.

Remarque : La méthode de l’étude du bon point de vue par la sphère englobante est reprise dans [Dje91]. Il ajoute, pour son étude, un graphe dont les sommets sont les objets de la scène et les arêtes correspondent à une relation du type « cache de x% dans la direction d ». Ce graphe est mis en place à la création des objets. De ce fait, sa méthode est intermédiaire entre les deux familles. Par contre, sa méthode, pour sélectionner le meilleur point de vue, ne se base que sur les projections des objets ce qui n’est pas toujours suffisant.

4.2.3 Critique comparée des deux familles

Les méthodes “a priori” paraissent plus intéressantes car elles ne nécessitent pas de parcours supplémentaires de la scène (dans le cas, par exemple, d’une structure hiérarchique). Mais les méthodes “a posteriori” sont utiles pour :

· trouver une vue si les autres méthodes ont échoué ;

· confirmer ou affiner les résultats des méthodes “a priori” ;

· proposer un deuxième point de vue.

Les méthodes “a priori” ne peuvent s’appliquer qu’à des scènes produites de manière déclarative alors que les méthodes “a posteriori” peuvent s’appliquer à n’importe quel type de scène (utilisables dans n’importe quelle application de CAO). De plus, [Ple91] montre que les méthodes “a priori” ne donnent pas toujours un résultat correct (à cause des propriétés de placement). Il est alors nécessaire de considérer plusieurs points de vue, d’utiliser des tests de validité approximatifs ou une méthode “a posteriori”.

4.3. Bons modes de visualisation

4.3.1 Propriété et visualisation

[Pou94b] propose deux catégories de propriétés :

1. Les propriétés qui ne demandent pas de modification de la scène. Ce sont généralement les propriétés géométriques. A ce niveau, le calcul d’un bon point de vue et d’un bon éclairage est suffisant.

2. Les propriétés qui nécessitent un traitement préalable de l’ensemble des données pour être montrées. Ce sont les propriétés ayant trait à la constitution de la scène. Elles doivent être calculées à partir des données. Elles nécessitent un procédé qui permet de mettre en évidence ce qui n’est pas visible. Il faut interpréter visuellement les données.

Le calcul d’un bon point de vue n’est pas toujours suffisant pour “voir” certaines propriétés de la forme. Un certain nombre de techniques de visualisation sont employées pour améliorer l’observation de la forme.

Pour choisir le ou les modes de visualisation utiles, [Col90b] considère trois types de propriétés (du point de vue de la visualisation bien sûr) :

1. Les propriétés internes. Leur mise en évidence nécessite l’observation de l’intérieur de la forme.

2. Les propriétés externes. Elles sont visibles pour un observateur situé à l’extérieur de la forme.

3. Les propriétés non observables. Leurs caractéristiques ne sont ni géométriques ni réellement visuelles.

4.3.2 Propriétés internes

La visualisation des propriétés internes peut être effectuée par plusieurs méthodes :

· Un affichage partiel de la forme. Dans ce cas, seules les parties indispensables sont affichées.

· Un mixage des modes de visualisation. On peut ainsi mélanger divers modes de visualisation (visualisation en fil de fer, avec élimination des parties cachées, transparence...). Cela permet de masquer les parties qui gênent la visualisation d’une propriété.

· Un affichage de la forme en “négatif”. La forme est visualisée en “négatif”. Par exemple, certaines cavités peuvent être visualisées de cette manière (la forme est transparente et la cavité est “pleine”).

· Un découpage de la forme. La forme est découpée en morceaux afin d’entrevoir les propriétés cachées. On peut, par exemple la couper en tranches (cf. [Char87], [Ker89], [Pou94b] et [Fau95]). Cette technique s’utilise pour visualiser les trous à l’intérieur d’une matrice de voxels. Le nombre de coupes sera fonction du nombre de trous.

· Un traitement spécifique. La forme est transformée pour mettre en évidence une ou plusieurs propriétés. Par exemple, [Pou94b] propose de visualiser la propriété de connexité en utilisant un squelette de la forme ou une couleur (ou un objet) particulier par composante.

· Des informations supplémentaires. [Pou94b] propose, pour mettre en évidence les répartitions de voxels dans l’espace, d’afficher des diagrammes rendant compte de la répartition pour un axe donné. L’idée est donc d’analyser la forme selon certains critères. Cette analyse est proposée à l’utilisateur sous forme de statistiques (analyse factorielle...) ou de diagrammes (courbes, histogrammes...). Le système opère une véritable analyse de données.

4.3.3 Propriétés externes

La visualisation des propriétés externes peut être faite à l’aide de méthodes de visualisation classiques : le fil de fer, l’élimination des parties cachées, le squelette... Combinées avec un bon point de vue, ces techniques sont le plus souvent suffisantes. Il est possible, afin de souligner telle ou telle propriété d’utiliser d’autres techniques comme l’emploi de fausses couleurs, de textures...

Bien entendu, les techniques de visualisation réaliste (lancer de rayons, radiosité...) doivent pouvoir présenter la forme telle que l’imagine l’utilisateur afin qu’il juge subjectivement la forme proposée (ne pas utiliser en premier lieu car elle est très coûteuse en temps). Pour ces propriétés, il est envisageable d’utiliser aussi l’éclairage de la forme en plaçant de façon judicieuse la ou les sources lumineuses. Ce placement peut être automatique en utilisant les techniques présentées pour la recherche d’un bon point de vue.

4.3.4 Propriétés non observables

Les propriétés non (ou très difficilement) observables doivent, quant à elles, être visualisées avec des techniques supplémentaires. Les techniques utilisant un traitement spécifique et des informations supplémentaires sont valables. Il faut avoir recours à la symbolisation à l’aide de symboles, images, textures ou palettes de couleurs. C’est le cas pour visualiser des propriétés physiques ou thermiques par exemple.

4.3.5 Equivalence visuelle

Dans certaines situations (animation, visualisations approximatives...), l’utilisateur veut obtenir rapidement une forme solution. Parfois, la définition de la scène est trop précise par rapport aux conditions d’affichage courant (objet plus petit qu’un pixel par exemple).

Pour gérer ces cas, [Ple91] propose une méthode de visualisation prenant en compte la scène, sa structuration et la structure de données associée. Il propose la notion d’équivalence visuelle : deux scènes sont visuellement équivalentes si leurs images sont identiques, c’est-à-dire si leurs différences ne peuvent se voir.

L’objectif est de réduire le nombre de solutions engendrées ou proposées à l’utilisateur pour ne pas tout visualiser. La génération s’arrête à un niveau de détail donné au-dessous duquel les différences ne sont pas visibles.

Cette technique est donc bien adaptée à la structure de données hiérarchiques. Les niveaux de détail peuvent être déterminés par l’utilisateur ou par l’algorithme de visualisation en fonction de l’équivalence visuelle. Ils peuvent varier selon les différents composants de la scène générée (en fonction de la distance de l’observateur, des intérêts de l’utilisateur...).

Dans le cas où l’on utilise une structure de donnée hiérarchique, [Ple91] propose aussi une méthode de visualisation spécifique tirant profit des structures hiérarchiques et des niveaux de détails. Cette méthode s’inspire de l’algorithme de visualisation réaliste de lancer de rayons et de l’optimisation associée appelée l’expansion sélective. Elle a l’avantage, en plus de ceux du lancer de rayons, de réduire le temps de calcul, de tirer parti des niveaux de détail (qui peuvent être variables) et d’être applicable à tout ou partie de la scène.

4.3.6 Remarque

Il faut faire attention à l’algorithme de visualisation utilisé (Watkins, lancer de rayons, radiosité...) car s’il est mal choisi, il risque de ne pas faire ressortir certaines propriétés de la forme. L’algorithme utilisé doit être rapide (quand c’est possible, utilisation d’algorithmes spécialisés et du parallélisme), facile à manipuler et fiable (il doit permettre de visualiser tous les types de scène).

4.4. Présentation d’une solution

Pour bien appréhender une forme, un bon point de vue n’est pas suffisant. Il est en effet intéressant d’avoir plusieurs autres vues à sa disposition. On peut obtenir :

· des bons points de vue suffisamment différents (utilisation de techniques de calcul “a priori” et “a posteriori” simultanément ou séparément) ;

· des angles de vue (même s’ils ne sont pas considérés comme de bons points de vue) qui montrent une ou deux propriétés particulièrement essentielles ;

· des modes de visualisation (utilisation de techniques de visualisation rapides et approximatives ou réalistes et précises) pour montrer la forme sous différents aspects ou pour souligner certaines propriétés.

Pour faciliter le choix d’une solution, hormis la représentation visuelle, il est intéressant de pouvoir connaître toutes ses caractéristiques, toutes ses propriétés (même celles qui n’étaient pas demandées) ainsi que des informations basées sur l’analyse des données (diagrammes, tableaux...) quand cela est possible.

4.5. Comparaison des solutions

Malgré la diversité de l’information acquise, décrire et visualiser une solution ne suffit pas toujours pour pouvoir faire son choix. Il faut aussi avoir la possibilité de comparer plusieurs solutions entre elles. Cette comparaison doit être visuelle et avoir lieu entre toutes les solutions qui semblaient également intéressantes. Il est bon aussi de connaître les propriétés essentielles qui les différencient ainsi que les coefficients de ressemblance.

[Paj94b] décrit un outil permettant cette prise de connaissance des solutions. Elle propose des outils de mise en page (une page correspond généralement à un écran) des différentes informations visuelles ou textuelles. Cela permet de visualiser à l’écran plusieurs vues d’objets ainsi que les textes correspondant aux listes des propriétés qui ont conduit à l’obtention des solutions. L’utilisateur doit pouvoir choisir la disposition des vues sur l’écran et indiquer de quelle manière il souhaite les voir utilisées. Les vues sont groupées et ordonnées. A chaque groupe est associé un module de l’application. Plusieurs outils sont proposés pour les communications entre les vues, les modules et les procédures d’interfaces spécifiques. La construction d’une page se fait de manière déclarative à l’aide d’un vocabulaire spécifique. La génération d’une solution se fait en mode échantillonnage. L’utilisateur peut modifier l’organisation d’une page d’une manière déclarative à l’aide d’un vocabulaire de modification spécifique.

On peut se demander si, dans ce cas, la partie modélisation déclarative est vraiment utile. En effet, [Paj94b] indique elle-même, qu’en général, le nombre de fenêtres manipulées est faible. De plus, la manipulation se fait en deux dimensions (avec en plus une notion de plan pour les recouvrements de fenêtres). Il reste à montrer que ce type de génération est plus efficace et facile à utiliser que des outils classiques de CAO en 2D (utilisation de la souris, positionnement standard...).

5. Création d’une solution

Une fois la solution obtenue, l’utilisateur (ou une machine spécialisée) doit pouvoir la construire lui-même (maquette, sculpture, objet réel...). Il faut donc que l’application décrive l’objet retenu ainsi que son mode de fabrication.

C’est ce qui a été réalisé par [Paj94b] dans son application FiloTableaux. Une fois le tableau de fils choisi, le système propose un patron et un mode de construction afin que l’utilisateur puisse le réaliser lui-même. Il va donc lui fournir les informations indispensables à la conception : éléments, quantités, mode de construction, images d’aide (patron) et propriétés principales utiles...

Pour cela, il faut aussi mettre en place un vocabulaire spécifique afin d’éviter toute ambiguïté dans le mode opératoire et suffisamment courant pour être compris par l’opérateur.

6. Conclusion

Nous avons constaté que des outils de prise de connaissance des solutions correspondant à une description sont indispensables. Un certain nombre de méthodes et principes ont été étudiés (bon point de vue, bon mode de visualisation...). Cependant, il rester encore beaucoup de travail à faire sur ce thème. Il faudrait analyser plus finement, entre autres, des méthodes pour gérer convenablement un grand nombre de solutions, des règles permettant d’associer une propriété possédant des caractéristiques données et une technique de visualisation, exploiter les outils de navigation dans une scène (VRML)…

Dans les chapitres I.2, I.3 et I.4, nous avons présenté les différentes phases d’un modeleur déclaratif. Une présentation plus synthétique de ces phases peut être trouvée dans [CDMM97].

Nous allons nous attarder maintenant à un thème qui est en train de prendre de plus en plus d’importance en modélisation déclarative : l’introduction de techniques d’apprentissage.

Chapitre I.5
Apprentissage

1. Introduction

Selon [Vig89], il n’y a pas de définition formelle du processus d’apprentissage. De façon intuitive, à partir de connaissances de base et de données expérimentales, on définit ce processus à l’aide des activités essentielles concernées telles que :

· acquisition de connaissances,

· développement de stratégies et de résolution,

· organisation des connaissances,

· découvertes de nouveaux faits et théories.

Selon [Cham95], l’apprentissage a pour objectif l’amélioration des performances des systèmes. Cela peut être la réalisation de tâches de façon plus rapide, plus précise, en un mot efficace.

Comme nous allons pouvoir le constater, il n’y a pas beaucoup de travaux concernant l’utilisation de techniques d’apprentissage dans les divers projets.

[LMM89] définit les intérêts des possibilités d’apprentissage :

· garder une trace de ce qui a été exploré pour, d’une part, retrouver rapidement des objets connus, d’autre part, ne pas revoir des objets ou classes d’objets déjà connus ;

· conserver des points de vue intéressants, lorsque le choix automatique d’un bon point de vue a nécessité de longs calculs ;

· enrichir le système d’exploration par l’incorporation de nouvelles règles de description, ou de nouvelles propriétés (avec les règles d’élagage associées) ;

· pouvoir adapter les modalités d’exploration en fonction de ce que connaît le système, c’est-à-dire si, à un moment donné, une meilleure voie d’exploration est trouvée (découverte d’arbres d’exploration mieux adaptés) ou si de nouvelles contraintes sont ajoutées, le modeleur doit pouvoir adapter sa stratégie de recherche de solutions.

L’apprentissage permet aussi une gestion des erreurs. Il donne la possibilité d’améliorer le parcours des arbres pour éviter d’aboutir à une forme déjà vue ou menant sûrement à un échec.

Il y a deux objectifs principaux à l’apprentissage :

1. économiser du temps de calcul (et donc avoir des réponses plus rapides) en réutilisant des recherches faites précédemment ;

2. ajouter de nouvelles potentialités au système, sans avoir à réécrire de nombreuses lignes de programme.

Nous allons nous intéresser aux techniques d’apprentissage dans les différentes phases d’un modeleur déclaratif. D’abord, nous étudierons quelques techniques d’apprentissage du vocabulaire (section 2). Puis, nous présenterons l’étude de ces techniques dans les arbres d’exploration (section 3) et dans les arbres de construction (section 4).

2. Apprentissage de nouveau vocabulaire

2.1. Introduction

La description d’une forme est basée sur l’utilisation d’un certain vocabulaire. Or, l’utilisateur doit pouvoir, pour éviter de répéter une description complexe ou pour coller mieux à son habitude, définir de nouveaux mots.

[Chau92] propose deux techniques d’apprentissage de vocabulaire :

1. l’apprentissage syntaxique,

2. l’apprentissage sémantique.

2.2. Apprentissage syntaxique

Cette technique d’apprentissage consiste à créer de nouveaux mots à partir d’une combinaison de mots connus. Cette combinaison peut comprendre des conjonctions, des disjonctions ou des négations de termes. [Bel94] appelle cette idée l’apprentissage par instruction.

2.3. Apprentissage sémantique

Ce type d’apprentissage est nécessaire quand :

· la sémantique d’un mot n’est pas juste par rapport à l’idée que s’en fait l’utilisateur,

· apparaît le besoin d’un nouveau terme ne pouvant être une combinaison de mots connus (apprentissage syntaxique insuffisant).

Le système doit donc donner la possibilité de proposer :

· la sémantique d’un mot connu afin de la modifier,

· des outils pour créer une propriété (nom et sémantique).

[Chau92] propose de permettre à l’utilisateur de modifier lui-même les paramètres que peut avoir une propriété ou de créer entièrement une propriété (nouveau nom et paramètres adaptés).

C’est possible dans le cas particulier de l’application de [Chau92]. Mais cela sous-entend que l’utilisateur maîtrise totalement les valeurs des paramètres, connaît le mode de génération et la structure de données. [Chau94] corrige cet inconvénient en proposant un apprentissage par l’exemple : l’utilisateur donne une forme respectant cette nouvelle propriété (systèmes du type apprentissage par analogie ([Ric87]) ou apprentissage par détection des similarités, aussi appelé apprentissage de type SBL (Similarity Based Learning) (cf [ASc94])).

[Chau94] propose aussi un apprentissage lié au refus répété de solutions. Dans ce cas, le système remet en cause la valeur de la propriété nettement refusée pour en déduire une autre qui serait susceptible de plaire.

2.4. Apprentissage par formation des concepts

Cette technique d’apprentissage est présentée par [Bel94] pour enrichir les possibilités de description (aussi appelé apprentissage par concept et a pour objectif de résoudre des problèmes de classification ([Ric87])). Elle permet de spécialiser le logiciel de conception et de constituer une bibliothèque de concepts. Un concept est associé à la définition de toute scène, objet ou attribut. Les définitions de ces éléments (en l’occurrence des règles) forment le dictionnaire.

Il y a deux catégories de concepts : les attributs et les objets. Les attributs sont regroupés en classes (attributs portant sur, sinon une même propriété, du moins des propriétés similaires). Chaque classe est organisée de façon hiérarchique (en fonction, par exemple, des valeurs de paramètres).

Chaque nouvel objet est considéré comme un nouveau concept. Un objet peut être décrit de plusieurs manières. A partir de ces différentes descriptions, le système va définir le concept par généralisation (apprentissage de type SBL). Le procédé de généralisation consiste en une recherche d’un optimum à l’intérieur de l’espace de définition des concepts qui couvrent l’ensemble des exemples.

Les critères de généralisation sont :

· la solution la plus générale est celle qui possède le moins d’objets dans sa description,

· si deux objets constituant la scène ont des propriétés de forme différentes, alors ces propriétés seront négligées dans la définition.

Les étapes de la généralisation sont les suivantes :

· Affiner le modèle à comparer. Les règles précises sont remplacées par des règles imprécises. Les descripteurs sont extraits afin de reconnaître les concepts attributs qu’ils sous-entendent. Cette reconnaissance se fait par l’intermédiaire d’un arbre de décision dont les feuilles sont les classes d’attributs et les nœuds, les descripteurs de comparaison.

· Généraliser avec le modèle existant. Le système construit un arbre de description pour le modèle déjà existant et pour le nouvel exemple. Chaque nœud coïncide avec une partie dans la décomposition hiérarchique. Il construit ensuite un troisième arbre à partir des deux précédents en tenant compte des deux critères de généralisation. En particulier, le premier critère permet l’arrêt de l’arbre si l’un des arbres descend à un niveau plus bas que l’autre. Les propriétés inter-scènes pour les objets élagués sont alors négligées. L’arbre résultant est alors l’intersection des deux arbres.

Pour les attributs des nœuds du nouvel arbre, on a :

· tous les attributs communs aux deux arbres sont repris,

· si deux attributs sont de même classe, l’attribut résultat sera l’attribut moyen dans la hiérarchie de la classe.

Cette nouvelle définition, généralisation des deux arbres, est alors mise dans le dictionnaire. Cependant, il faut remarquer que [Bel94] ne précise pas comment utiliser ces concepts généralisés.

2.5. L’apprentissage dans une phase de description

Dès maintenant, nous pouvons déduire un classement des techniques d’apprentissage à mettre en place lors de la phase de description.

L’apprentissage du vocabulaire se situe à deux niveaux :

1. le niveau syntaxique (l’utilisateur construit des homonymes, des antonymes, des synonymes ...) ;

2. le niveau sémantique (l’utilisateur définit ses propres propriétés).

Ce dernier niveau peut être divisé en deux catégories :

1. L’apprentissage sémantique “faible”. Il se contente de redéfinir certains paramètres de propriétés et de modificateurs. Il donne, par exemple, de nouveaux intervalles de validité, de nouvelles valeurs pour les qualificatifs...

2. L’apprentissage sémantique “fort”. L’utilisateur peut décrire, d’une manière ou d’une autre, les nouvelles procédures qui permettront de vérifier de nouvelles propriétés. L’apprentissage peut être totalement pris en charge par l’utilisateur (il entre directement le code de la vérification ainsi que toutes les propriétés) ou assisté par le système (à l’aide d’exemple et de contre-exemples...). Les caractéristiques de ces nouvelles propriétés (afin de déterminer leur comportement pour d’éventuels Réductions des contrôles ou élagages) seront données par l’utilisateur (mais cela demande de sa part une connaissance des techniques de traitement) ou analysées par le système.

Une solution, pour la première catégorie, pourrait être la suivante : l’utilisateur, pendant une phase d’apprentissage, détermine lui-même ce qui lui semble correspondre le mieux aux différents termes utilisés. Ainsi, ils correspondront à sa propre conception du monde. Cette solution n’a pas encore été étudiée.

Cependant, nous pouvons imaginer certaines solutions possibles :

· le classement de solutions caractéristiques par rapport au vocabulaire ;

· l’énumération de solutions à classer jusqu’à obtention d’une cohérence ;

· sa propre définition des différentes notions par proposition de valeurs ou d’intervalles...

A tout cela, nous pouvons ajouter la possibilité de définir de nouveaux éléments de base (impérativement, par contraintes ou d’une manière déclarative à l’aide d’une application spécialisée) et de nouvelles techniques de construction.

3. Apprentissage dans les arbres d’exploration

Pour [Col90] l’apprentissage a pour double objectif de conserver de plus en plus de connaissance et devenir de plus en plus efficace. Le but est en fait de mettre en place une construction dynamique de l’arbre d’exploitation. L’apprentissage permettra aussi de montrer des formes nouvelles qui ne sont encore jamais apparues au cours de toutes les explorations précédentes.

[Col90] propose d’utiliser des techniques d’apprentissage afin de mieux déterminer le réglage des intervalles optimaux pour le déclenchement d’une propriété à partir d’une garde. L’apprentissage effectue ce réglage au cours des explorations en fonction des propriétés, du niveau dans l’arbre et des régions de l’univers. Il est aussi possible d’améliorer le parcours de l’arbre pour qu’il se construise dynamiquement, nœud par nœud, en choisissant celui qui semble le meilleur.

Il propose aussi un mécanisme d’estampillage permettant la gestion d’une “mémoire” associée à une notion d’interdiction d’actions élémentaires. Ceci permet de se souvenir des actions qui ont mené à un échec afin de ne pas les refaire.

Cette dernière notion a été plus particulièrement étudiée dans [Cham94] et [ChC94]. L’apprentissage est basé sur l’acquisition de connaissances lors de la détection d’échecs ou de succès pendant l’exploration (système de type EBL (Explanation Based Learning) ou apprentissage par recherche d’explication ([ASc94])). Ici, l’élément de connaissance est une configuration locale. Cette technique est intéressante si l’on note que, dans une exploration, il existe des configurations locales identiques que l’on retrouve dans l’arbre. Le système doit refaire plusieurs fois le même calcul pour les propriétés locales. L’objectif de cette technique est de faire l’étude de la propriété lors de la première rencontre de la configuration et d’exploiter le résultat sur les autres formes. Grâce à cela, il devrait y avoir une diminution du nombre de détections, une limitation du nombre de formes induites et la réalisation de formes rejetée a posteriori serait évitée. Globalement, tout cela doit réduire le temps d’exécution. La connaissance est attachée localement. Elle évolue en fonction du parcours de l’arbre et est conservée le plus longtemps possible.

L’objectif est d’arriver à dire que, pour une forme donnée, si l’on effectue une opération donnée à un endroit précis alors le système sait qu’il y a la propriété et il est inutile de la vérifier mathématiquement. Pour une configuration locale d’une forme, si la propriété est détectée, le système créé une connaissance qui contiendra les facteurs locaux responsables. Lorsque les mêmes phénomènes se reproduisent, il peut se servir de cette connaissance.

Dans le cas où la propriété prend en compte un facteur symétrique, le système génère une connaissance et sa réciproque. Ces deux connaissances seront gérées ensembles. Une meilleure solution serait de créer, plutôt que deux connaissances, une seule plus générale.

Une connaissance est créée chaque fois que l’on détecte mathématiquement certaines propriétés. Elle est liée à la configuration locale. Elle est désactivée lorsque la configuration disparaît. Elle est réactivée lorsqu’une configuration identique réapparaît.

Cette connaissance sera présente dans tout le sous-arbre ayant pour racine le nœud où apparaît toute la configuration (système d’arbre de génération dont tous les nœuds sont formes complètes). De plus, la connaissance pourra être remontée lors du retour-arrière. Si la configuration locale disparaît, la connaissance reste sous forme désactivée. Le nombre de remontées autorisées sera appelé le seuil. La connaissance va donc se retrouver dans d’autres sous-arbres. Une remontée consiste à déplacer la connaissance dans la forme en fonction de sa construction.

Une fois la configuration locale disparue (provisoirement peut-être), la connaissance associée est désactivée. Elle n’est réactivée que lorsqu’un des facteurs réapparaît, c’est-à-dire si l’on commence à se retrouver dans la même situation (même endroit, même ordre de construction...). Au-delà du seuil, la connaissance et sa ou ses réciproques meurent, c’est-à-dire disparaissent définitivement. Lorsqu’elle redescend, elle reprend exactement le même chemin. Ceci signifie que la connaissance ne redevient active que si la configuration réapparaît exactement dans les mêmes conditions, c’est-à-dire que les configurations locales, modulo une rotation ou une translation, sont considérées comme différentes.

Cet apprentissage est basé sur :

· la création de connaissances déduites sur des configurations locales,

· l’association de la connaissance à des entités spécifiques,

· l’activation et la désactivation des connaissances au fur et à mesure de l’évolution des formes,

· la transmission des connaissances,

· une durée de conservation des connaissances réglable (seuil), ce qui permet de modifier le niveau d’apprentissage souhaité,

· la suppression de la connaissance.

Cet apprentissage ne concerne que certaines propriétés. Globalement, celles qui seraient susceptibles d’utiliser de l’apprentissage doivent nécessiter des calculs très lourds, avoir un potentiel d’élagage important et dépendre de configurations précises.

[Cham94] et [ChC94] donnent une évaluation de cette méthode. Les résultats liés à l’apprentissage et aux connaissances correspondent aux attentes.

En résumé, les principaux résultats sont les suivants :

Ä plus le seuil augmente (c’est-à-dire plus la connaissance reste longtemps) ;

Ä plus le temps de recherche des propriétés baisse ;

Ä moins le nombre de connaissance de connaissances est important ;

Ä plus le nombre d’élagage est grand ;

Ä plus l’utilisation des connaissances est importante ;

Ä plus le nombre de calculs de la propriété est faible.

Par contre, ils ont mis en évidence un problème majeur : plus le seuil augmente, plus le temps total de l’étude augmente (sauf dans certains cas particuliers qui n’ont pas été étudiés).

Finalement, on obtient l’effet inverse de celui désiré, la méthode ralentit le traitement. Les raisons avancées sont basées sur des problèmes de gestion de la connaissance acquise. D’une part, celle-ci est stockée sous forme de listes. Or, le nombre de connaissances à gérer augmente avec leur temps de vie et la gestion des listes de connaissances devient alors plus lourde. D’autre part, on s’aperçoit qu’une grande partie des connaissances ne sert pratiquement pas (disparaissent avant d’être utiles, sont générées lors de situations exceptionnelles...) et, donc, encombrent le système. Pour améliorer le rendement, il faudrait pouvoir extraire les connaissances les plus efficaces.

Ils notent aussi que l’augmentation du seuil n’apporte plus rien à partir d’un moment. Pour leur étude, ils se sont aperçus que le seuil limite est de 3. Au-dessus, les différences sont minimes. Ceci n’est pas expliqué.

Leur conclusion semble importante. Leur technique semble bien gérer la connaissance mais cette même gestion est très (trop) coûteuse. L’introduction de la technique d’apprentissage coûte plus en gestion qu’elle ne rapporte en optimisation (élagages, études moins nombreuses...) surtout s’il y a remonté des connaissances (seuil ≥ 0). Il convient donc d’être prudent et de ne pas introduire systématiquement l’apprentissage. Ces techniques ne doivent être utilisées que si cela en vaut la peine.

A leurs remarques, nous pouvons en ajouter une autre. Les connaissances qu’ils gèrent sont trop spécifiques. Une connaissance concerne une propriété locale mais elle prend en compte la technique de construction. Elle utilise le chemin de construction afin de reconnaître le cas. Il serait intéressant de pouvoir généraliser la connaissance afin qu’elle soit disponible pour d’autres parties de la scène. Cette idée contribuerait à diminuer le nombre de connaissances à gérer. Enfin, ils soulignent qu’un des problèmes se trouve dans la gestion des connaissances. Les connaissances sont stockées dans des listes. Ne serait-il pas plus efficace, lorsque c’est possible, d’utiliser une structure arborescente ?

4. Apprentissage dans les arbres de construction

4.1. Introduction

[MaM89] puis [MaM90] proposent la notion de règle d’apprentissage. Ces règles vont permettre l’implantation des techniques d’apprentissage dans le système à base de règles. Ils proposent une technique d’apprentissage qui consiste à mémoriser les formes ayant demandé une déduction longue ou complexe. En les associant à un fait ou à une règle, cela permettra une déduction plus rapide si, dans une prochaine génération, les mêmes conditions se présentent. Le nombre de solutions à étudier s’en trouvera diminué.

Cette technique permet aussi l’ajout de nouvelles propriétés et donne la possibilité de faire référence à d’autres formes dans une description : avec la notion de “ressemble à”. Des outils de comparaison de formes (voir [Mar90] et [Pou94b]) devront, bien évidemment, être disponibles.

Il sera possible aussi de généraliser à partir d’une forme. En prenant les faits caractéristiques d’une forme ou d’une classe de formes, il sera possible de créer de nouvelles règles associées à une nouvelle propriété. Si cette propriété est demandée, les règles ajouteront les faits caractéristiques. Par contre, si elle est refusée, elles vérifieront qu’aucun fait caractéristique n’apparaît (sinon mise en place d’un élagage).

Les règles de suppression et d’apparition pour la gestion des propriétés dans un système à base de règles ([Col90]) apparaissent comme une certaine forme d’apprentissage (ou plus exactement une forme de mémorisation). En effet, les règles de suppression permettent une mémorisation des propriétés disparues et les règles d’apparition utilisent cette mémoire pour retrouver des propriétés.

[Ple91] propose d’introduire dans son système la notion d’apprentissage. L’apprentissage doit être commandé par l’utilisateur. Il n’y a pas d’apprentissage au niveau du moteur mais au niveau des règles et des faits.

Il propose alors plusieurs possibilités dont les deux suivantes :

· L’ensemble de règles qui définit la scène est remplacé par plusieurs ensembles de règles ne comportant plus de règles de forme, de placement, de taille mais uniquement des règles de création de faits utiles avec des valeurs numériques bien précises : celles retenues par le concepteur. Mais cette solution n’est pas souple.

· L’apprentissage joue au niveau du fait de départ qui définit l’espace de travail. Les paramètres de départ sont choisis en fonction des choix habituels de l’utilisateur. Cela est facile à mettre en oeuvre et réduit le nombre de scènes à générer.

[BoP94] et [Bel94] proposent deux techniques d’apprentissage complémentaires (selon [Bel94]) que nous allons étudier maintenant.

4.2. Apprentissage par réduction du niveau de détail

[BoP94] propose la technique d’apprentissage suivante :

· L’utilisateur choisit un niveau de détail donné.

· Le système lui propose les scènes à ce niveau.

· L’utilisateur choisit celle qu’il préfère.

· Le système lui propose alors des scènes basées sur l’exemple de la scène choisie en ajoutant à la description les paramètres fixés par l’exemple.

Nous pouvons faire quelques remarques sur cette solution. D’une part, la notion d’apprentissage n’est pas justifiée. Cette technique ressemble plus à une idée de génération dirigée par l’utilisateur. Le système descend d’un certain nombre de nœuds dans l’arbre (P niveaux en profondeur) et propose toutes les solutions qu’il trouve. L’utilisateur en choisie une. Le système reprend alors sa recherche sur P niveaux et redemande une solution. Et ainsi de suite jusqu’à obtenir une solution satisfaisante pour l’utilisateur. Ce genre de technique va éviter de parcourir tout l’arbre mais risque de laisser des solutions de côté (obligation de choisir une branche donnée).

[Bel94] reprend cette idée en proposant de ne pas se bloquer sur une scène donnée, mais seulement sur une partie de la scène. L’utilisateur indique la partie de la scène qui lui semble intéressante. Toutes les solutions proposées auront alors cette partie plus ou moins commune.

4.3. Apprentissage par réseaux de neurones pour la décomposition hiérarchique

[BoP94] propose d’utiliser des réseaux de neurones afin d’améliorer l’élagage des arbres de construction (technique de type SBL).

Cette technique doit se dérouler en deux phases :

1. la phase d’apprentissage où l’utilisateur choisi quelques scènes pour servir d’exemple ;

2. la phase de génération classique où le réseau de neurones joue le rôle de filtre sur les scènes en construction afin de ne garder que celles s’approchant des scènes choisies.

Le réseau de neurones est constitué, en fait, d’un arbre de réseaux de neurones totalement identique à l’arbre de description. Chaque réseau de cet arbre est indépendant.

L’évaluation d’une scène (ou d’une sous-scène) commence seulement si le nœud parent l’autorise. Une scène (sous-scène) est acceptée si, dans l’ordre, le réseau associé puis les nœuds fils l’acceptent. Pour les propriétés de placement relatif, il faut associer un réseau qui sera activé en premier lieu lors de l’étude de la scène.

Chaque réseau de nœud est constitué d’autant de mini-réseaux que de propriétés à vérifier. Chaque mini-réseau est constitué d’une sortie et d’autant d’entrées que de paramètres pour la propriété.

Lors de la phase d’apprentissage, le système détermine l’intervalle de validité pour les sorties de chaque propriété. La méthode de détermination des intervalles n’est pas précisée par [BoP94] ni par [Bel94], mais il semble qu’elle est basée sur la valeur moyenne de la sortie pendant l’apprentissage, compte tenu d’une certaine incertitude.

Figure 8. Mini-réseau pour une propriété i ayant 3 paramètres

Les poids sont mis à jour selon la formule suivante : p_i+1 = p_i - | Me_i+1 - e_i+1 | où Me_i+1 est la moyenne des entrées, e_i+1 l’entrée du nouvel exemple et p_i le poids précédent et p_i+1 le nouveau poids. Si p est inférieur à une valeur limite, il devient nul. L’objectif de cette formule est de diminuer l’importance des liaisons pour lesquelles les entrées changent souvent.

[Bel94] signale qu’il serait bon d’améliorer les entrées du réseau ainsi que de choisir une formule plus sensible aux changements des entrées.

Lors de la génération classique, une forme est acceptée par un réseau si toutes les sorties de ces mini-réseaux sont dans leurs intervalles respectifs.

Les neurones étudiés ici n’utilisent pas de notion de seuil. De plus, la sortie d’un neurone demande à être étudiée afin de déterminer si le résultat est correct. Il serait préférable d’ajouter une ou plusieurs couches au réseau afin de lier tous les mini-réseaux. Ainsi, la décision de valider ou non la scène serait aussi prise par le réseau. Nous aurions alors un réseau à ∑n_i entrées (n_i étant le nombre de paramètre de la propriété i) et une sortie. Cette sortie serait à 1 si la scène est correcte et à 0 sinon.

D’autre part, il serait intéressant d’étudier une technique qui semble similaire mais moins lourde à gérer : l’utilisation d’une fonction d’évaluation. Cette fonction serait une combinaison des paramètres, chacun associé à un poids. Les poids seraient attribués selon la même formule (apprentissage par ajustement des paramètres selon [Ric87]). Une scène serait valide pour une valeur de la fonction dépassant un certain seuil.

La phase d’apprentissage nécessite de commencer à parcourir l’arbre de construction. Cette technique va donc demander de construire deux fois certaines solutions. Si la phase d’apprentissage parcourt une partie de l’arbre qui ne sera pas parcourue par la phase de génération classique, des problèmes se posent encore. Combien d’exemples sont nécessaires afin d’obtenir des résultats suffisamment fiables ? Est-elle rentable si les exemples n’ont que peu de points communs (filtre très faible et coût d’étude important) à cause de choix peu cohérents ? Si les solutions sont peu nombreuses, cette technique est-elle intéressante (surtout si c’est pour ne retrouver que les exemples) ? En effet, si les exemples trouvés sont déjà les solutions, la génération devient inutile et l’on passe la recherche en phase d’apprentissage. Le problème revient alors à connaître le nombre de solutions possibles. Ceci est le plus souvent impossible. Le problème est encore aggravé si ces solutions se trouvent en fin de parcours de l’arbre de construction. Enfin, faut-il attendre que la scène soit entièrement construite pour l’analyser (nécessité de connaître les fils pour étudier les placements relatifs...) ? Si c’est le cas, il va donc y avoir, pour chaque scène, deux parcours d’arbre. Ceci peut être coûteux si l’arbre est important.

5. Conclusion

L’introduction des techniques d’apprentissage en modélisation déclarative est assez récente. Le besoin s’en est toujours fait sentir mais les études sérieuses ne datent que de 1994. Elles portent sur toutes les phases de la modélisation déclarative. L’objectif est aussi bien d’améliorer le confort de l’utilisateur potentiel que d’enrichir les connaissances du système et d’améliorer ses performances. Ces travaux ne sont pas encore très concluants et demandent à être approfondis.

[Cham95] et [Cham96] proposent une très bonne synthèse des différentes techniques d’apprentissage en IA et analyse leur application possible en modélisation déclarative. Il propose quelques méthodes applicables au niveau de la description, de la génération et de la prise de connaissance. Il préconise, à juste titre, l’utilisation simultanée de différentes techniques complémentaires. Cependant, actuellement, les méthodes d’apprentissage ne sont utilisable efficacement que par les spécialistes du domaine (nous avons montré la difficulté de mettre au point de telles méthodes). Il serait donc préférable, plutôt que d’essayer de « bricoler » une technique fonctionnant plus ou moins bien, de leur faire appel. Actuellement, seul [Mou96b] utilise efficacement une adaptation des algorithmes génétiques pour l’exploration.

Chapitre I.6
Conclusion

Tout au long de cet exposé, nous avons pu constater que les travaux en modélisation déclarative sont nombreux et récents. Ils portent sur les problèmes de saisie d’une description, les techniques pour optimiser la génération ainsi que sur les méthodes de visualisation. Ces recherches ont montré, à travers les différentes applications, la faisabilité de cet outil de conception. Elles ont, pour l’instant, essentiellement porté sur les algorithmes de génération.

Cependant, il reste encore beaucoup de travail à faire. Au niveau pratique, il faudrait étudier la possibilité de mettre en place en système réellement utilisable. Mais surtout au niveau théorique, il reste un certain nombre de point important à étudier :

· utilisation de méthodes d’apprentissage performantes ;

· formalisation et organisation des connaissances (propriétés et structures de donnée des scènes) ;

· étude plus poussée du traitement de la description et du vocabulaire (du point de vue langage naturel) ;

· étude plus approfondie des méthodes de prise de connaissance (en particulier sur les possibilités de mettre en relation des techniques de visualisation et les caractéristiques des propriétés) et, surtout, d’exploration des solutions ;

· études de techniques de parallélisation…

· étude de l’utilisation d’un algorithme mixte (arbre de génération avec système expert et même résolveur de contraintes) afin d’améliorer la génération des scènes.

Remarque : Depuis quelque temps, les travaux de synthèse se sont multipliés sous l’impulsion du groupe GEODE. C’est une équipe du GDR-PRC AMI dont le thème est la modélisation déclarative. Elle est constituée de l’équipe MGII de l’Institut de Recherche en Informatique de Nantes, du CERMA de l’École d’Architecture de Nantes, et de l’équipe de synthèse d’images de l’École des Mines de Nantes. En particulier, le sous-groupe « schéma » qui s’est intéressé à effectuer une synthèse des modeleurs déclaratifs du point de vue de l’utilisateur et qui a mis en évidence les processus de conception à l’aide de modeleurs déclaratifs ([CDMM97]).

Le nombre de travaux en modélisation déclarative est actuellement très important. Il devient nécessaire de regrouper toutes ces études afin de proposer une base de développement de modeleurs déclaratifs. Nous proposons donc une plate-forme pour la construction d’applications déclaratives : CordiFormes.

Avant cela, il est indispensable de bien structurer les connaissances. Nous nous proposons donc de mettre en place un formalisme permettant de représenter et gérer les connaissances d’un modeleur déclaratif. Un des fondements des applications déclaratives est la possibilité de donner des descriptions imprécises ou floues. Nous nous attacherons donc dans la partie 2 à construire un formalisme de représentation des connaissances et des propriétés basées sur les sous-ensembles flous.