3. Mots et monoïdes
libres
Intuitivement, un mot est un ensemble de symboles d'un alphabet placés
les uns après les autres donc une suite de lettres (ou chaîne de
caractères, dans une terminologie plus informatique).
| 
Symbole, Alphabet,
Mots &
Mot vide
|
Un symbole
est une brique élémentaire, un atome.
Un alphabet
A est un ensemble fini et non vide de symboles.
Un mot (ou chaîne)
sur un alphabet A est une suite finie de lettres de A.
Si [p] désigne la suite d'entiers (1, 2, ..., p), un mot m
est une application de [p] dans A (m : [p] → A) pour un certain
p de N. p est appelé la longueur
du mot m, notée |m|. Intuitivement, p est le nombre
de symboles du mot.
Le mot vide est
le mot de longueur 0, c'est-à-dire ne contenant aucun symbole. Il
est souvent noté ε. |
Remarque : Dans la suite, les alphabets seront décrits
comme des ensembles de symboles (entre accolades),
éventuellement composés de plusieurs caractères. Les symboles
représentés par des signes de ponctuation seront entre quotes.
Par exemple, A1 = {1}, A2 = {0, 1}, A3
= {., -, /}, A4 = {0, 1, 2, ..., 9}, A5 = {a, b, ...,
z}, A6={a,b,ch,';',','} et A={a,b,c} sont
des alphabets et abbc, aaaa, bc,
ε sont des mots sur l'alphabet
A, respectivement de longueur 4, 4, 2 et 0.
 Soit l'alphabet
{a,b,c,h,ch,';',','}. Les mots ch (|ch|=1)
et c ⊕ h ≡ ch (|c ⊕ h|=2)
sont théoriquement différents. Il n'y a donc (théoriquement) pas
d'ambiguïté sur le mot ch. En pratique, cette
ambiguïté est à lever. Dans le suite de ce cours, nous prendrons
volontairement des alphabets qui ne présenterons pas cette ambiguïté.
Soit l'alphabet
{a,b,c,h,ch,';',','}. Les mots ch (|ch|=1)
et c ⊕ h ≡ ch (|c ⊕ h|=2)
sont théoriquement différents. Il n'y a donc (théoriquement) pas
d'ambiguïté sur le mot ch. En pratique, cette
ambiguïté est à lever. Dans le suite de ce cours, nous prendrons
volontairement des alphabets qui ne présenterons pas cette ambiguïté.
Par convention (valable dans la suite du document), nous posons :
- Que a, b, c, d, e, f, 0, 1... désignent des symboles.
- Que t, u, v, x, y, z désignent des chaînes.
- La chaîne aaaa est aussi notée a4.
Par conséquent, a0=ε.
- Le symbole m(i) désigne le i-ème symbole de la chaîne
m.
Dans la suite, nous définissons les mots comme les éléments
de monoïdes particuliers.
On peut définir sur les mots (ou chaînes) une opération
particulière : la concaténation. Intuitivement,
si x et y sont des chaînes, alors le résultat
de la concaténation de x et y est la chaîne xy.
Cette opération est associative : (xy)z=x(yz)=xyz (Les parenthèses
sont ici des symboles mathématiques et n'appartiennent pas à l'alphabet
de référence). De plus, la chaîne vide ε est un
élément neutre pour la concaténation. L'ensemble des mots
sur un alphabet donné peut ainsi être muni d'une structure de monoïde
. Ce type de monoïde, un peu particulier, est appelé monoïde
libre.
| 
Concaténation & monoïde libre
|
Étant
donné un alphabet A :
- On note A* l'ensemble de tous les mots sur A.
- Dans A*, on définit une opération dite produit
de concaténation ou simplement concaténation.
Elle est noté ⊕ ou plus souvent implicite (simple juxtaposition
des opérandes).
- Cette opération binaire est une loi de composition interne associative
définie de la façon suivante : soit u et v deux mots de
longueur p et q, la concaténation de u et v (dans cet ordre) est
le mot w de longueur p+q défini par w(i)=u(i) si 1 ≤ i ≤
p et w(i)=v(i) si p+1 ≤ i ≤ q. Autrement dit, w est construit par
juxtaposition des mots u et v, c'est-à-dire w = u ⊕ v = uv.
- ε est un élément neutre pour la concaténation.
- Le monoïde <A*, ⊕, ε> est appelé
le monoïde libre engendré par A.
|
Par exemple, si x=ab et y=cd, alors x ⊕ y = xy
= abcd. De plus, x ⊕ ε = ε ⊕ x = x
et, par exemple, (ab ⊕ cd) ⊕ ef = abcd ⊕ ef = abcdef =
ab ⊕ (cdef) = ab ⊕ (cd ⊕ ef).
Remarques :
- L'ensemble A* des mots ainsi construit est infini dénombrable.
- Les symboles de l'alphabet sont atomiques, ie : si a ∈ A, ∀
x,y ∈ A+ : a ≠ xy
- Il n'y a pas d'inverse pour l'opération de concaténation,
ie : si u ∈ A+, ∀ v ∈ A+ : uv ≠
ε

Théorème de la décomposition |
Tout
mot x (de longueur n=|x|) sur un alphabet A se décompose de façon
unique en x1 ⊕ x2 ⊕... ⊕ xn,
également noté x1x2...xn,
où ∀i ∈ [1..n], xi ∈ A. |
Démonstration
En deux mots, comme les symboles de l'alphabet sont des atomes, il n'est
pas possible de diviser un mot plus qu'au niveau de ces symboles. Si deux
divisions en symboles étaient possibles, cela voudrait dire qu'un symbole
peut être divisé et donc il ne serait pas atomique.
Ce théorème sert de base à beaucoup de démonstrations
par induction sur la longueur des mots.
Par exemple, avec A = {a,b,c} alors abbcabbc = a ⊕ b ⊕
b ⊕ c ⊕ a ⊕ b ⊕ b ⊕ c.
Remarque : Une chaîne sur un alphabet A peut également être
définie récursivement par :
- la chaîne vide ε est une chaîne sur A;
- si x est une chaîne sur A et a ∈ A alors la chaîne ax
et xa sont des chaînes (mots) sur A (Attention, dans le cas général,
ax ≠ xa);
- aucun autre objet n'est une chaîne sur A.
Cette définition
sert de base pour la démonstration de nombreuses propriétés
à propos des mots, par récurrence (induction) sur leur longueur.
L'idée générale est que pour montrer qu'une propriété
P est vraie pour tous les mots, il suffit de montrer que P
est vraie pour ε (cas de base) et que si P est vraie pour un mot x
(hypothèse de récurrence), alors elle est vraie pour ax,
∀ a.
|

Théorème de Levi |
Soit
t,u,v,w ∈ A*, si tu=vw alors il existe un unique (∃!) z ∈ A*
tel que :
- (v=tz et u=zw)
- ou (t=vz et zu=w)
|
Démonstration :
Pour bien comprendre ce théorème, comme souvent, un petit schéma
s'impose. t, u, v, w et z correspondent aux situations suivantes :
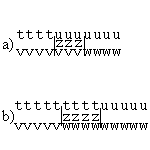
Pour le cas a), "zzz" correspond à ce qu'il faut ajouter aux
"t" pour atteindre la longueur des "v". Le cas b) est
symétrique.
Démonstration
plus formelle.
Notations :
- L'ensemble des mots (ou chaînes) de longueur n (pour n
∈ N) construits sur A est noté An (An
= {x1x2...xn | ∀ i, 1 ≤ i ≤
n, xi ∈ A}) . Par conséquent, toutes les chaînes
y de l'ensemble A3 ont pour longueur |y|=3.
- L'ensemble des chaînes de longueur finie et non nulle définies
sur A est noté A+= ∪n=1..∞ An
={x | ∃n ∈ N, n ≥ 1 et x ∈ An}.
Notons que A* = A+ ∪ {ε}
- Par convention, A0 est ε et donc A*=∪n=0..∞
An
Par exemple, si l'on considère l'alphabet A= {0,1} alors :
- A0={ε} ;
- A1 = A ={0, 1} ;
- A2 = {0,1}2 = {00, 01, 10, 11} ;
- A3 = {0,1}3 = {000, 001, 010, 011, 100, 101, 110,
111};
- ...
- A* = {0,1}* = {ε, 0,1, 00,01,10, 11,000, 001,
010, 011,..., 11111, ..., 1001101110...}.
- A+ = {0,1}+ = {0,1, 00,01,10, 11,000, 001, 010, 011,...,
11111, ..., 1001101110...}.
- si S = {ε,0, 00, 000, 0000, ...} = {0i} ⊂ A+
(avec ε=00) alors <S,⊕,ε> est le sous-monoïde
de <A*,⊕,ε> engendré
par {0}.
Remarque : Si c1 ∈ An et c2 ∈ Am
alors c1 ⊕ c2 ∈ An+m.
Exercices et tests :
Exercice 3.1. Donner la longueur
des mots suivants sur l'alphabet {a,b,c} :
- abcb
- abba
- ε
- bb

Exercice 3.2. Donner la longueur
des mots suivants sur l'alphabet {a,b,ch,','} :
- a,bbaa
- achbbaa

Exercice 3.3. Soient a, b des
symboles de A et u un mot de A*. Montrer que si ua=bu alors a=b et u ∈ a*.


jeudi, 11/12/03 11:00
![]()