4. Les automates finis généralisés

4.1. Principes

Les AFNs sont très utilisés pour les traitements séquentiels sur des suites de symboles (mots, phrases, suites d'actions...) à cause de la facilité de mise en oeuvre du procédé et des avantages qu'ils offrent dans le cas de modifications ou d'extensions d'un traitement.

Cependant, on utilise souvent des AFNs généralisés qui ne se contentent pas de reconnaître des chaînes de symboles, mais éventuellement qui les traitent au passage. Les généralisations classiques sont les suivantes :

  1. la tête de lecture reconnaît une classe de symboles (au minimum, une par symbole et toutes disjointes), et pas seulement un symbole (comme nous l'avons vu précédemment) ;
  2. un traitement particulier peut être associé à un état de la machine, ou à une transition, visant soit à produire un résultat, soit à modifier l'état de l'automate ;
  3. un traitement d'erreur est souvent prévu en cas de mauvaise analyse d'un symbole.

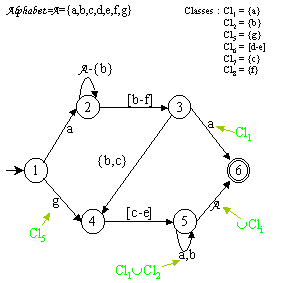
Dans le cadre des automates généralisés (cas 1), il est donc possible de simplifier les transitions en introduisant la notion de classe de symboles. La figure suivante montre comment les utiliser :


Automate avec classes de symboles

Une application illustrant cette généralisation concerne les "transducteurs" ("Machines séquentielles"). Un transducteur permet de réaliser une transduction de l'alphabet d'entrée vers un alphabet de sortie. Un transducteur est aussi appelé "Machine de Moore" lorsque la sortie est produite pour chaque état et "Machine de Mealy" lorsqu'elle est produite pour chaque transition.

4.2. Machine de Moore

Une machine de Moore est donc définie de la manière suivante :


Machine de Moore

Une machine de Moore est composée de la même manière qu'un automate d'état fini. Elle est défini par (A, A', Q, I, F, μ, μ') tel que :

  • A est l'alphabet d'entrée, ensemble fini, non vide de symboles ;
  • A' est l'alphabet de sortie, ensemble fini de symboles ;
  • Q est l'ensemble des états possibles pour la machine (fini et non vide) ;
  • I ⊆ Q est l'ensemble des états initiaux ou états de départ ;
  • F ⊆ Q correspond aux états finaux ou états d'acceptation ;
  • μ la fonction de transition telle que μ : A ∪ {ε} × Q → Q. Pour la configuration courante d'état et de symbole, μ(aj,qi)=qk signifie qu'on passe dans l'état qk et que le ruban est déplacé d'une case vers la gauche.
  • μ' une fonction de sortie telle que μ' : Q → A'. μ'(qi)=aj indique que le caractère aj est émis (ou imprimé) en entrant dans l'état qi.

Prenons comme exemple la machine suivante ({a,b,c,d,e,f,g},{1,2,3,4,5,6},{1},{6}, μ, {μ'(1)=0, μ'(2))1, μ'(3)=0, μ'(4)= 1, μ'(5)=0, μ'(6)=1}) avec μ décrite par le graphe de transitions suivant :


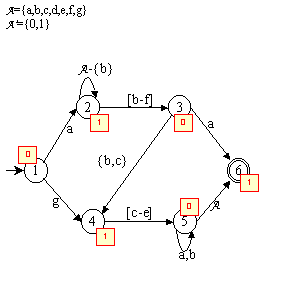
Machine de Moore

Sur cette machine, les mots suivants sont acceptés et donnent :

4.3. Machine de Mealy

Une machine de Mealy est définie de la manière suivante :


Machine de Mealy

Une machine de Mealy est composée de la même manière qu'un automate d'état fini. Elle est défini par (A, A', Q, I, F, μ) tel que :

  • A est l'alphabet d'entrée, ensemble fini, non vide de symboles ;
  • A' est l'alphabet de sortie, ensemble fini de symboles ;
  • Q est l'ensemble des états possibles pour la machine (fini et non vide) ;
  • I ⊆ Q est l'ensemble des états initiaux ou états de départ ;
  • F ⊆ Q correspond aux états finaux ou états d'acceptation ;
  • μ la fonction de transition telle que μ : A ∪ {ε} × Q → Q × A'. Pour la configuration courante d'état et de symbole, μ(aj,qi)=(qk,al') signifie qu'on passe dans l'état qk, que le symbole al' est généré (imprimé) et que le ruban est déplacé d'une case vers la gauche.

Prenons comme exemple la machine suivante ({a,b,c,d,e,f,g},{1,2,3,4,5,6},{1},{6}, μ) avec μ décrite par le graphe de transitions suivant :


Machine de Mealy

Sur cette machine, les mots suivants sont acceptés et donnent :

4.4 Equivalence des machines


Equivalence entre Machine de Mealy et Machine de Moore

Soit une machine de Moore, notée Mo, qui imprime x au départ et une machine de Mealy, notée Me. Les deux machines sont équivalentes, Mo ≡ Me, si pour tout mot d'entrée, Me imprime w et Mo imprime xw.

A partir de cette définition, deux théorèmes sont démontrables. tout d'abord :


Théorème Moore->Mealy

Pour toute machine de Moore, il existe une machine de Mealy tel que les deux machines sont équivalentes.

Démonstration :

La démonstration se fait par construction de Me à partir de Mo.

Puis :


Théorème Mealy->Moore

Pour toute machine de Mealy, il existe une machine de Moore tel que les deux machines sont équivalentes.

Démonstration :

La démonstration se fait par construction de Mo à partir de Me.

 

Exercices et tests :

Exercice 4.1. Donner la machine de Mealy permettant de calculer le complément binaire.
Par exemple, "101" donne "010", "001010" donne "110101"...

Solution

Exercice 4.2. Ecrire l'automate généralisé permettant de compter le nombre d'occurrences du facteur "ac" pour des mots de l'alphabet A={a,b,c} contenant au moins deux "a" consécutifs. Aide

Solution

mercredi, 26/11/03 9:40