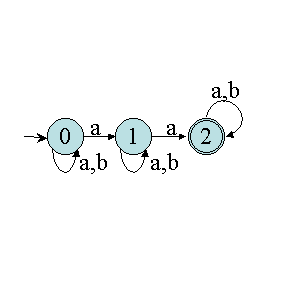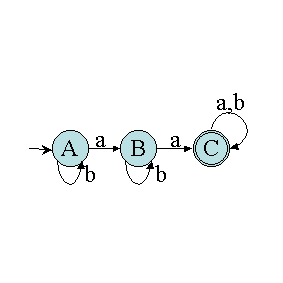Après avoir introduit les automates finis non déterministes (AFN) et déterministes (AFD), nous allons tout d'abord présenter un algorithme permettant de passer d'un AFN à un AFD. Il en exite plusieurs, plus ou moins performants. Nous ne présenterons ici qu'un seul algorithme qui nous semble suffisamment simple pour avoir une idée de la méthode abordée.
A tout AFN comportant des ε-transitions, il est possible de faire correspondre un AFN équivalent, c'est-à-dire reconnaissant le même langage, sans ε-transition.
La fonction ε-fermetureμ(a,q) détermine tous les états dans lesquels peut passer l'automate dans l'état q après (1) zéro ou plus ε-transitions, (2) une transition sur a puis (3) zéro ou plus ε-transitions. L'algorithme permettant de déterminer l'ε-fermeture pour un ensemble d'états sera présenté plus loin.
Il n'est pas difficile de comprendre que la complexité d'un algorithme de reconnaissance basé directement sur un AFN est beaucoup plus importante (beaucoup d'états, états inutiles et surtout non-déterminisme) que celle basée sur un AFD.
Or, il est possible de montrer que, pour tout AFN, il existe un AFD équivalent, c'est-à-dire reconnaissant le même langage. Il est donc intéressant de chercher à transformer un AFN en AFD. Pour cela, nous allons présenter une méthode simple appelée la méthode par construction des sous-ensembles.
L'algorithme de transformation d'un AFN en AFD n'est possible que parce qu'on peut montrer qu'à un AFN donné il existe un AFD équivalent.
|
|
Soit T=(A, Q, I, F, μ) un AFN qui reconnaît le langage L=L(T) alors il existe un AFD T'=(A, Q', I', F', μ') tel que L'=L(T')=L. |
Dém. (constructive) : on construit T' de la façon suivante :
On peut montrer que (w,S) —i/T'→ (ε, S') si et seulement si S'={p | ∃ q ∈ S : (w,q) —i/T→ (ε, p)}. Cas particulier : (w, {q0}) —i/T'→ (ε, S') pour S' ∈ F' si et seulement si (w, q0) —i/T→ (ε, p) pour p ∈ F. En effet :
Nous présentons maintenant un algorithme qui construit à partir d'un AFN un AFD qui reconnaît le même langage. Cet algorithme, appelé souvent par construction des sous-ensembles, est utile pour faire simuler un AFN par un programme.
L'idée générale sur laquelle se base la transformation d'un AFN en AFD est que chaque état de l'AFD correspond à un ensemble d'états de l'AFN. Un état courant de l'AFD correspond à l'ensemble des états possibles de l'AFN qui sont atteints avec la même chaîne d'entrée. L’AFD "simule" le parcours "en parallèle" des états pour un mot donné.
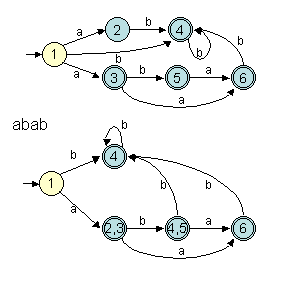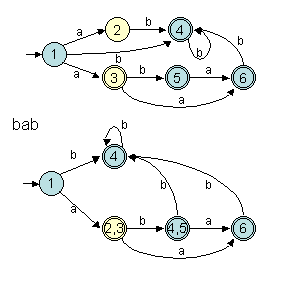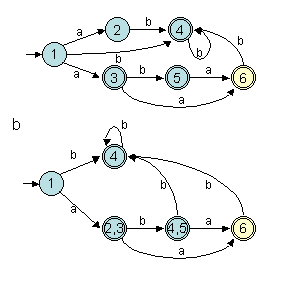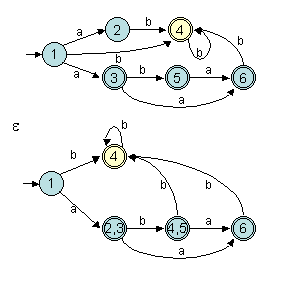
L'exemple suivant illustre la reconnaissance du mot "abab" sur deux automates équivalents l'un (celui du haut) non déterministe et l'autre (celui du bas) déterministe et obtenu par la méthode de construction des sous-ensembles. Le nom des états indiquent les états dans lesquels on arrive avec le parcours en parallèle du premier automate.
La construction d'un AFD à partir d'un AFN se base sur les définitions de l'ε-fermeture, permettant de supprimer les ε-transitions et d'une fonction Μ permettant de déterminer les états accessibles depuis un ensemble d'états par les transitions selon un symbole donné de l'alphabet.
|
L'ε-fermeture d'un état e ∈ Q d'un AFN T=(A, Q, I, F, μ), notée ε-fermeture(e), est l'ensemble des états de T accessibles depuis l'état e par 0, 1... n ε-transitions seulement. |
Par exemple, considérons l'automate T suivant :
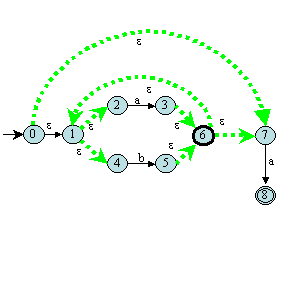
Calculons ε-fermeture(T,{6}).
μ(ε, 6) = 1 et μ(ε, 6) = 7 donc :
ε-fermeture(T,{6}) = {6} ∪ ε-fermeture(T,{1}) ∪ ε-fermeture(T,{7}).
μ(ε, 1) = 2 et μ(ε, 1) = 4 donc :
ε-fermeture(T,{1}) = {1} ∪ ε-fermeture(T,{2}) ∪ ε-fermeture(T,{4})μ(ε, 2) = ∅ donc ε-fermeture(T,{2}) = {2}
μ(ε, 4) = ∅ donc ε-fermeture(T,{4}) = {4}
Donc ε-fermeture(T,{1}) = {1, 2, 4}
μ(ε, 7) = ∅ donc ε-fermeture(T,{7}) = {7}
Donc ε-fermeture(T,{6}) = {1, 2, 4, 6, 7}
Le calcul de l'ε-fermeture d'un ensemble E est un processus typique de recherche dans un graphe d'un ensemble donné de noeuds. Dans ce cas, les états de E forment un ensemble donné de noeuds et le graphe est constitué uniquement des ε-transitions de l'AFN. Pour calculer l'ε-fermeture, on utilise une pile pour conserver les états dont les transitions n'ont pas encore été examinées.
Si l'on prend l'automate T précédent, Μ(a,{2,7}) = {3,8}.
L'algorithme construit la fonction de transition μ' de l'AFD T'=(A, Q', I', F', μ'). Chaque état de l'AFD est un ensemble d'états de l'AFN T=(A, Q, I, F, μ) et on construit μ' de telle manière que l'AFD simulera "en parallèle" tous les déplacements possibles que l'AFN peut effectuer sur une chaîne d'entrée donnée. On utilise les opérations définies ci-dessus pour garder trace des ensembles d'états de l'AFN.
On construit Q', I' et μ' de la manière suivante. Chaque état de Q' correspond à un ensemble d'états de T dans lesquels l'automate pourrait se trouver après avoir lu une suite de symboles en entrée en incluant les ε-transitions possibles avant ou après la lecture des symboles. L'état de départ I' est l'ε-fermeture de I. Un état de T' est un état d'acceptation si c'est un ensemble d'états de T qui contient au moins un état d'acceptation.
Compte-tenu de ce qui a été présenté à la section précédente, l'algorithme de construction d'un AFD T' = {A, Q', I', F', μ'} à partir d'un AFN quelconque T = {A, Q, I, F, μ} est le suivant :
Soit l'automate suivant :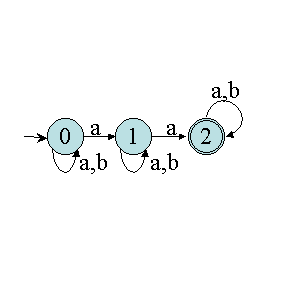 
La construction de l'AFD équivalent commence par la détermination de l'état initial (c'est un AFD, donc il n'y a qu'un seul état initial). Celui-ci est construit à partir de l'ε-fermeture de tous les états initiaux. Donc ici, I'={0}. A partir de là, on construit la table des transitions.
Phase 1 :
| μ | a |
b |
| A = {0} = I' |
Puis, on regarde vers quels états l'automate se trouve pour chacun des symboles de l'alphabet à partir de I'. Normalement, il faut faire l'ε-fermeture sur les états obtenus mais dans cet automate il n'y a aucune ε-transition. On les ajoute à la table s'ils n'y sont pas déjà.
Phase 2 :
| μ | a |
b |
| A = {0} = I' | {0,1} |
{0} |
| B = {0,1} |
Puis on fait la même chose pour chacun des états pas encore traités.
Phase 3 :
| μ | a |
b |
| A = {0} = I' | {0,1} |
{0} |
| B = {0,1} | {0,1,2} |
{0,1} |
| C = {0,1,2} |
C contient l'état 2 qui est final dans l'automate de départ. Donc C est un état final dans l'AFD obtenu.
Phase 4 :
| μ | a |
b |
| A = {0} = I' | {0,1} |
{0} |
| B = {0,1} | {0,1,2} |
{0,1} |
| C = {0,1,2} ∈ F | {0,1,2} |
{0,1,2} |
Finalement, le tableau est rempli, l'automate est terminé. On obtient l'automate suivant :
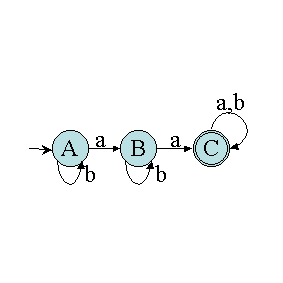
Remarque : Cette méthode ne comporte pas de difficultés particulières. La seul difficulté est que le nombre d'ensembles d'états peut être assez grand ainsi que la dimension de ces ensembles. Par conséquent, il n'est pas rare de faire des erreurs d'étourderie (la où la machine ne risque pas d'en faire !).
Prenons comme nouvel exemple un automate comportant des ε-transitions :
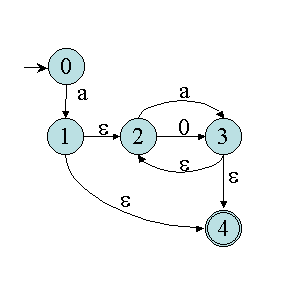
L'algorithme passe par les phases suivantes :
Phase 1 :
| μ | a |
0 |
| A = {0} = I' |
Phase 2 :
| μ | a |
b |
| A = {0} = I' | {1,2,4} |
∅ |
| {1,2,4} = B ∈ F | ||
| ∅ = C |
L'état en vert dans l'ensemble {1,2,4} est l'état dans lequel on arrive directement depuis l'état 0. Les autres sont ceux obtenus après ε-fermeture.
Phase 3 :
| μ | a |
b |
| A = {0} = I' | {1,2,4} |
∅ |
| {1,2,4} = B ∈ F | {3,2,4} |
{3,2,4} |
| ∅ = C | ||
| {2,3,4} = D ∈ F |
Phase 4 :
| μ | a |
b |
| A = {0} = I' | {1,2,4} |
∅ |
| {1,2,4} = B ∈ F | {3,2,4} |
{3,2,4} |
| ∅ = C | ∅ |
∅ |
| {2,3,4} = D ∈ F |
Phase 5 :
| μ | a |
b |
| A = {0} = I' | {1,2,4} |
∅ |
| {1,2,4} = B ∈ F | {3,2,4} |
{3,2,4} |
| ∅ = C | ∅ |
∅ |
| {2,3,4} = D ∈ F | {3,2,4} |
{3,2,4} |
Le tableau est terminer donc l'automate aussi. L'automate obtenu est le suivant :
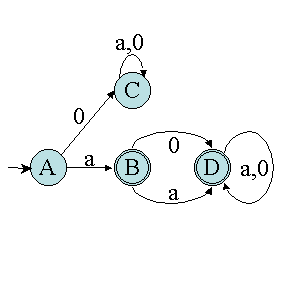
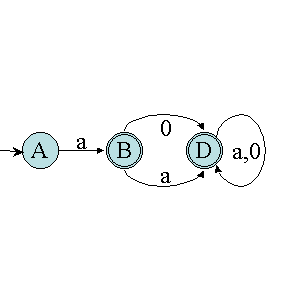
A noter l'état C qui est un état puits. Il est possible de ne pas l'ajouter et de ne pas remplir les cases qui correspondent. Ceci donne alors :
| μ | a |
b |
| A = {0} = I' | {1,2,4} |
|
| {1,2,4} = B ∈ F | {3,2,4} |
{3,2,4} |
| {2,3,4} = C ∈ F | {3,2,4} |
{3,2,4} |
8.7. Simulation directe d'un AFN
Il est possible d'effectuer une reconnaissance de chaîne donnée directement à partir de l'AFN sans passer par une déterminisation.
Cet algorithme construit dynamiquement les sous-ensembles. Il calcule une transition depuis l'ensemble courant d'états vers le prochain ensemble d'états en deux étapes. D'abord, il détermine l'ensemble de tous les états accessibles depuis l'ensemble courant par une transition sur le caractère courant. Ensuite, il calcule l'ε-fermeture, c'est-à-dire tous les états qui peuvent être atteints par zéro ou plusieurs ε-transitions.
Exercices et tests :
Exercice 8.1. Soit l'automate suivant sur l'alphabet {a,b,c} :
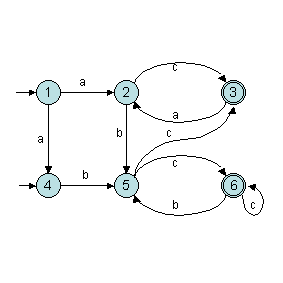
Donner l'automate déterministe équivalent par la méthode
de construction des sous-ensembles (donner le détail de la méthode).
Exercice 8.2. Soit l'automate suivant sur l'alphabet {a,b} :
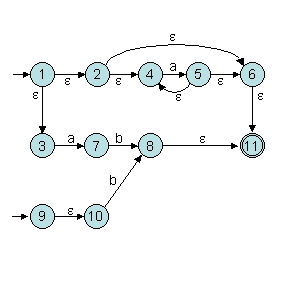
Donner l'automate déterministe équivalent par la méthode
de construction des sous-ensembles (donner le détail de la méthode).
Exercice 8.3. Soit l'automate suivant sur l'alphabet {a,b,c} (images issues de JFLAP ; avec ce logiciel les ε-transitions sont notée λ) :
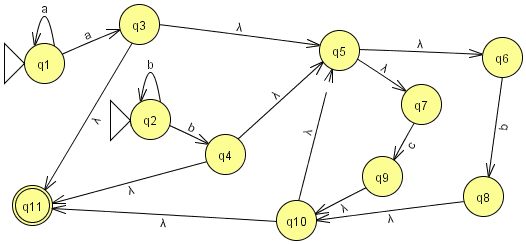
Donner l'automate déterministe équivalent par la méthode
de construction des sous-ensembles (donner le détail de la méthode).
mercredi, 17/12/03 12:35
