 Chapitre
5
Chapitre
5 
 Solution
de l'exercice 3.5
Solution
de l'exercice 3.5 
Donner les automates finis qui reconnaissent les mots des langages suivants
sur le vocabulaire {a,b} :
- le langage des mots avec un nombre pair de "a" et un nombre
impair de "b"
La description du langage est assez simple mais l'automate n'est pas forcément
facile à construire. Il faut considérer un automate comme
un machine de Turing qui, à tout moment est dans un état donné.
Il est possible d'associer à un état (dans le sens des Machines
de Turing) un "état" dans le sens commun, c'est-à-dire
indiquant où on en est dans la reconnaissance du mot.
Dans ce langage, les mots sont composés uniquement de "a"
et de "b". Au cours du parcours d'un mot, il est possible de maintenir
la connaissance de la parité du nombre de chaque symbole utilisé.
Autrement dit, à tout moment il est possible de savoir si l'on a
rencontré un nombre pair ou impaire de "a". Il en est de
même pour "b".
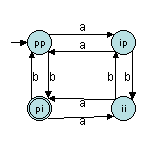
En poussant un peu plus l'analyse, seulement 4 situations sont possibles
: (1) nombre de "a" pair et nombre de "b" pair, (2)
nombre de "a" pair et nombre de "b" impair, (3) nombre
de "a" impair et nombre de "b" pair et finalement (4)
nombre de "a" impair et nombre de "b" impair. Donc,
la machine ne pourra être que dans 4 états par rapport à
l'objectif recherché. Donc l'automate possède 4 états
qui correspondent aux 4 situations. Avant de commencer l'analyse d'un mot,
la machine n'a vu aucun "a" et aucun "b" donc l'état
initial sera la situation (1). L'objectif étant d'accepter les mots
avec un nombre pair de "a" et un nombre impair de "b",
l'état final correspondra donc avec la situation (2). Ensuite, la
rencontre des "a" et des "b" fera passer d'une situation
à une autre. Aussi, nous obtenons l'automate suivant :
- le langage des mots ne contenant pas deux occurrences de "a"
successives.
Pour construire cet automate, deux approches sont possibles : (1) déterminer
les situations qui ne produisent pas deux "a" successifs ou (2)
"calculer" l'automate à partir de celui qui produit systématiquement
deux "a" successifs. Quelle que soit la méthode, éventuellement
en enlevant des états qui n'apportent rien (2), nous obtenons l'automate
(1) suivant :
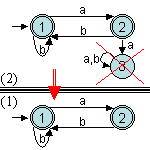
Nous verrons que la méthode (2) sera automatisable.
mardi, 25/11/03 11:12

