5. Représentation des grammaires hors contexte

A propos des grammaires hors contextes, il existe diverses présentations standard pratiques aussi bien pour les règles des grammaires que pour les dérivations qu'elles permettent. Nous donnons dans cette section deux normes de présentation des règles, puis la représentation usuelle des dérivations sous forme d'arbre.

5.1 Représentations des règles de production

Il existe donc plusieurs manières de représenter les règles d'une grammaire.

Textuellement, la norme BNF ("Backus-Naur-Form") est la plus utilisée. Elle est particulièrement utile pour analyser un langage défini par une grammaire hors-contexte (et donc aussi pour une grammaire linéaire). Les symboles non terminaux sont encadrés par des guillemets ("..." ou <<...>>), les symboles terminaux ne sont pas distingués (parfois les non-terminaux sont en majuscule et les terminaux en minuscule). L'axiome est la partie gauche de la première règle énoncée. La disjonction est notée par une barre verticale ( | ). La flèche des règles est remplacée par le signe "::=". Par exemple, le tableau suivant illustre la forme BNF pour les règles {S → bA ; A → aA ; A → a}.

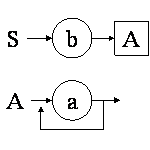
Il existe aussi une représentation graphique des règles en utilisant les diagrammes de Conway. Elle décrit graphiquement les grammaires hors-contexte. Il permet de regrouper des règles et de mettre en évidence les phénomènes récursifs. La partie gauche des règles est notée à gauche du schéma. Les symboles terminaux sont écrits dans des cercles et les symboles non terminaux sont écrits dans des rectangles. Une chaîne du langage est formée en parcourant les flèches et en recueillant les symboles rencontrés. La figure suivante montre les diagrammes de Conway pour la grammaire précédente.

Diagrammes de Conway pour les règles {S → bA ; A → aA ; A → a}

5.2 Arbres de dérivations

Rappelons que tout mot a du langage engendré par une grammaire G peut être obtenu par une dérivation S =+⇒ a avec a uniquement composé de vocabulaire terminal (a ∈ L(G) ⊆ V_T*). Une telle dérivation peut être représentée par un arbre de dérivation (appelé aussi "arbre syntaxique" ou "arbre d'analyse"). L'idée consiste à associer à chaque règle R : A → X₁ ... X_n de la grammaire, où A ∈ V_N et ∀ 1 ≤ i ≤ n, X_i ∈ V, la structure d'arbre suivante :

La correspondance entre arbres et dérivations est alors la suivante :

• Une dérivation directe A =R⇒ X₁ ... X_n est représentée par l'arbre ci-dessus.
• Et une dérivation de la forme A =n⇒ Y₁ ... Y_i-1 Y_i Y_i+1 ... Y_m =R⇒ Y₁ ... Y_i-1X₁ ... X_mY_i+1 ... Y_m est représentée par l'arbre associé à A =n⇒ Y₁... Y_m, dans lequel on remplace le symbole non terminal correspondant à Y_i par l'arbre associé à R.

Par exemple, en considérant les règles R1 : A → BaC, R2 : B → b et R3 : C → c, à la dérivation A =R1⇒ BaC =R2⇒ baC =R3⇒ bac correspond l'arbre suivant :

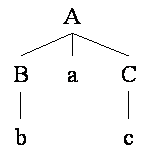
On peut remarquer que la représentation des dérivations sous forme d'arbres ne mémorise pas l'ordre dans lequel les règles sont appliquées, lorsque ces applications n'interfèrent pas. Par exemple, l'arbre ci-dessus correspond également à la dérivation A =R1⇒ BaC =R3⇒ Bac =R2⇒ bac.

Si l'on prend la grammaire G₂ et le mot "000111", nous avons l'arbre de dérivation suivant :

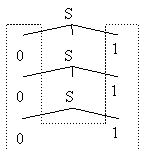
De façon générale, un arbre de dérivation d'un mot du langage engendré par une grammaire représente une façon de dériver ce mot à partir de l'axiome. La racine de l'arbre est l'axiome, ses feuilles sont les symboles (terminaux) du mots, et ses noeuds internes représentent les applications de règles. Notons que l'arbre de dérivation d'un mot n'est pas toujours unique. Une grammaire est dite ambiguë si au moins un mot dans son langage a plus d'un arbre de dérivation.

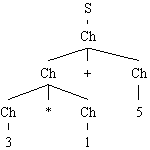
Par exemple, soit la grammaire G₆= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, *}, {S, A}, R}, avec R :

• S → Ch
• Ch → Ch + Ch | Ch * Ch
• Ch → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Par cette grammaire, nous pouvons obtenir pour le mot "3*1+5" les arbres de dérivation suivants :

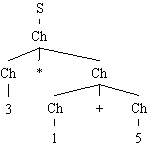Notons que ces deux arbres correspondent bien à deux façons différentes d'appliquer les règles qui cette fois, ne sont pas équivalentes. Intuitivement, l'arbre de gauche correspond à l'interprétation (3*1)+5 tandis que l'arbre droit correspond à 3*(1+5). L'ambiguïté dans les grammaires n'est donc pas un problème anodin, mais son étude approfondie sort du cadre de ce cours.