Dans les chapitres précédents, nous avons présenté une introduction à la théorie des langages et des automates. Ces notions ne sont pas seulement des éléments théoriques abstraits mais sont aussi des outils performants trouvant leur utilité dans de nombreux de domaines. Nous allons présenter ici une utilisation dans le domaine du traitement de langages à syntaxe contrainte (langages de programmation) ou souple (langage naturel). Dans un premier temps, nous étudierons la gestion des langages, et surtout l'utilisation des automates dans le cadre du processus de transformation d'un programme formulé dans un langage de programmation donné vers un langage compréhensible par une machine : c'est le processus de compilation. Puis, nous donnerons quelques éléments liés à l'analyse du langage naturel. Enfin, nous terminerons par la présentation d'autres domaines d'application.
La compilation est l'étude de la traduction de programmes écrits dans un langage de programmation (C, PASCAL, FORTRAN...), en des programmes équivalents écrits dans un langage de plus bas niveau (machine ou cible).
Un langage est formé d'un ensemble de phrases qui permet de désigner des objets d'un certain domaine sémantique ou univers et des actions portant sur ces objets.
Une phrase est un assemblage de mots appelés symboles dont l'ensemble constitue le vocabulaire du langage. Chaque mot ou symbole résulte de la concaténation d'une suite finie de signes ou caractères. Un symbole est la plus petite sous-séquence de signes chargée de sens que l'on peut classer suivant trois catégories :
Dans le cadre de l'informatique, de nombreux logiciels admettent en entrée des langages soumis à des règles d'écritures précises appelées règles syntaxiques.
Par exemple pour un SGBD, le langage d'interrogation d'une base de données permet de gérer les éléments de la base. Le logiciel doit contrôler la validité des commandes d'interrogation de la base (analyse syntaxique) puis est amené à exécuter des traitements spécifiques, ou actions, qui entraînent la recherche dans la base d'informations pour construire la réponse.
Dans ce cas, l'analyseur syntaxique dirige ou "pilote" le logiciel et on parle de programmation dirigée par la syntaxe. C'est une méthode de programmation en tant que telle.
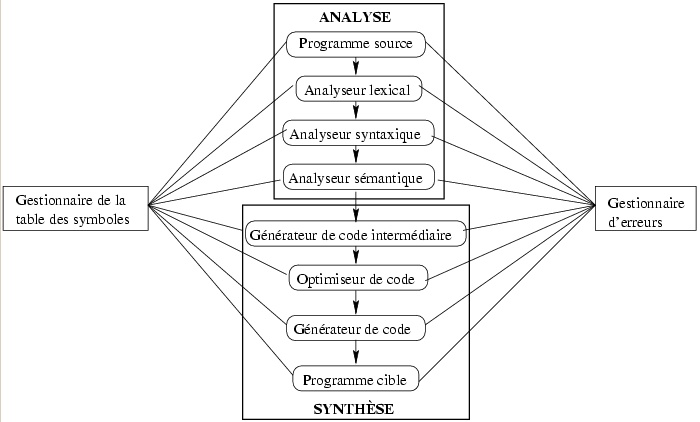
De façon générale, un compilateur est un programme qui lit en entrée un programme écrit dans un langage appelé <<langage source>>. Puis, il le traduit dans un programme équivalent dans un langage différent appelé langage cible. La compilation d'un programme se déroule en deux parties successives : l'analyse et la synthèse .

Elle permet de trouver la structure du programme à partir du texte du programme, c'est-à-dire d'une suite de caractères. L'analyse est uniquement dépendante du langage à traduire (indépendante du langage cible). Nous distinguons les trois phases d'analyse suivantes :
Au cours de ce processus d'analyse, un rôle important du compilateur est de signaler à son utilisateur, la présence d'erreurs dans le programme source via des messages d'erreurs. Par exemple, les erreurs peuvent être :
Après l'analyse du programme source vient la partie synthèse. Elle permet de traduire la structure du programme en prenant en compte les possibilités du langage cible (optimisation). Elle dépend du langage cible (choix des constructions machines, ressources disponibles...) et de la définition du langage compilé (c'est-à-dire du sens associé aux structures du programme : la sémantique du langage).
Elle peut se décomposer selon les phases suivantes :
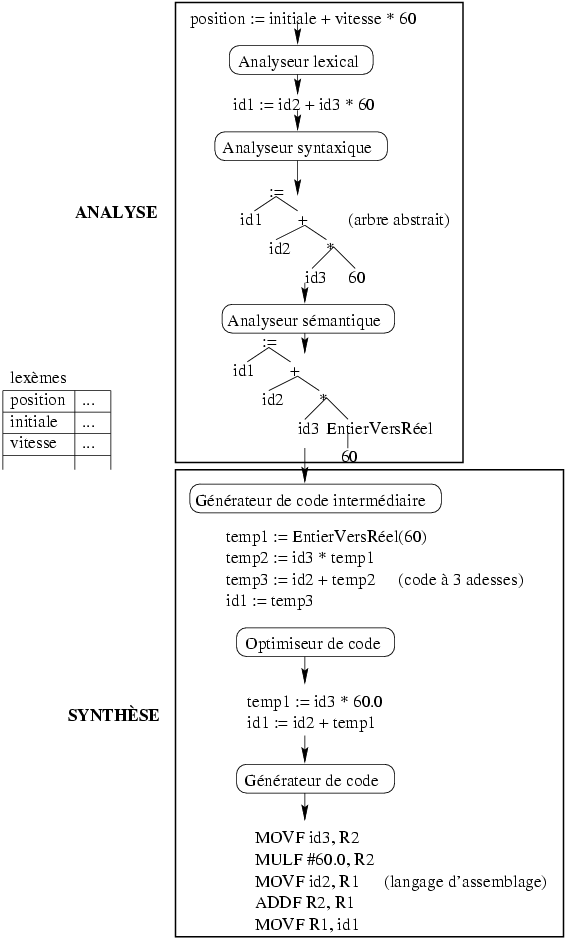
Voici un exemple du processus de compilation d'une instruction d'affectation et de calcul : "position := initiale + vitesse * 60;"
Par exemple : Pascal (vers du P-CODE ou du langage machine), C, Ada... sont des langages compilés.
La production d'un code machine destiné à être exécuté par le système procure une grande rapidité d'exécution parce qu'il peut être optimisé en exploitant au mieux les caractéristiques de l'architecture de la machine sur lequel il s'exécute. Mais cette approche révèle certains inconvénients :
Au lieu de produire un programme cible comme dans une technique de traduction normale, l'interprète effectue lui-même les opérations spécifiées par le programme source. Il exécute (interprète) un code intermédiaire qui est indépendant d'un code machine donné. L'interprète peut être écrit dans un langage évolué suffisamment universel pour que le changement de type d'ordinateur ne pose pas de trop gros problèmes. Si l'inconvénient majeur de l'interprète est sa lenteur, ses avantages sont sa portabilité et sa souplesse à l'exécution. En effet, l'utilisateur peut plus facilement intervenir durant l'exécution pour modifier son cours.
Par exemple : Basic, Lisp, Caml, Clips, Perl, Prolog, P-CODE... sont des langages interprétés.
Le compilateur Java génère du byte-code (indépendant de toute architecture) et non du code machine. Pour vraiment exécuter un programme Java, il faut utiliser un interpréteur qui exécute le byte-code généré. Un programme Java peut être exécuté sur tout système implémentant l'interpréteur Java et le runtime Java. Cet interpréteur et ce runtime implémentent à eux deux la machine virtuelle Java (ou JVM pour "Java Virtual Machine"). De ce fait, l'exécution d'un programme en Java est 20 fois plus lente qu'un programme équivalent en C. Cependant, la compilation en byte-code permet d'atteindre des temps d'exécution bien supérieurs aux programmes écrits en langages de scripts comme Tcl, Perl ou les shells UNIX.
Néanmoins, il existe des moyens de donner aux programmes en Java des performances très proches de celles d'un programme en C. Outre l'apparition de processeurs Java, il existe des compilateurs "just in time" (ie. "qui compilent au dernier moment") capables de compiler le byte-code Java en code machine dédié à un processeur particulier et ce en cours d'exécution. Cette génération de code machine est relativement simple à réaliser (prévue dès la conception du byte-code) et produit un code raisonnablement efficace. Ces compilateurs permettent de générer du code machine soit durant la génération du programme soit au moment de l'exécution. Dans ce dernier cas, la compilation s'effectue au premier passage dans le code en parallèle de la première exécution. Les passages suivants se font directement sur le code machine.
L'analyse lexicale ou lexicographique permet de déterminer les unités lexicales qui ont un sens. Cette analyse se base sur une grammaire. A l'aide de celle-ci, et donc du langage engendré, il est possible de mettre en place une procédure d'analyse d'une chaîne donnée. Sachant que la plupart des grammaires utilisées en analyse lexicale sont régulières, il est possible d'utiliser un automate fini pour cette analyse.
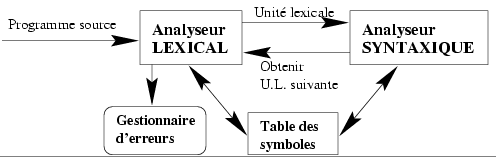
L'analyse lexicale est donc la reconnaissance d'un langage régulier (le plus souvent) et le codage des mots. Elle permet de découper le texte d'entrée en une suite de symboles.
Cette analyse utilise des expressions régulières, définissant les symboles (lexèmes) du langage, converties en un AFD minimal unique et un ensemble de couples : type de symbole / état final. L'analyse lexicale fait tourner l'AFD jusqu'à un état final et que le prochain caractère mène à une erreur.
Remarque : L'analyse lexicale fonctionne selon le principe de la plus grande correspondance : l'analyseur cherche à reconnaître la plus longue chaîne.
Les unités lexicales reconnues sont stockées dans la table des symboles. Cette table indique la classe lexicale (rôle de l'unité lexicale dans la phrase) et la catégorie du symbole (Par exemple, la table suivante).
Catégorie du symbole |
Classe lexicale |
mot clé |
classe de ce mot clé |
nombre |
C^{ste} |
chaîne |
C^{ste} |
autre mot |
identificateur |
Si le symbole est présent dans la table, celle-ci fournit son code lexical. Sinon, la classe de ce symbole est calculée. Son numéro est alors l'indice de la place libre suivante dans la table et l'information sur le symbole est rangée à cette place.
La gestion de cette table est un élément important de la phase d'analyse du programme. A l'accès associatif, on préfère souvent une gestion plus optimisée avec un accès direct. En pratique, on utilise souvent le "hashcoding".
Remarque : les mots clés du langage sont pré-enregistrés dans la table avec leur classe lexicale.
Les principales erreurs soulevées sont la rencontre d'un caractère non-autorisé ou le débordement de la table des symboles. Dans le premier cas, il suffit de "passer la main" à l'analyseur syntaxique avec "autre" comme classe de symboles. Dans le second cas, l'unique solution consiste à arrêter le programme (erreur fatale).
LEX est un outil pour construire des analyseurs lexicaux à partir de notations basées sur les expressions régulières. Il est souvent associé à YACC, un autre utilitaire Unix, basé aussi sur le langage C, pour produire des compilateurs. Lex sert à effectuer la phase d'analyse lexicale de la compilation, Yacc permet de réaliser la phase d'analyse syntaxique. Les autres phases de compilations sont définies en C.
La collaboration avec l'analyseur syntaxique s'effectue selon l'algorithme déjà présenté.
Il est possible de mettre en place une analyse syntaxique basée sur des grammaires régulières (donc utilisant un AFD). Les caractères du vocabulaire sont alors les symboles du langage. Sur les transitions, on associe alors des actions permettant de réagir à la présence d'un symbole (stockage de valeurs, affichage de résultats, calculs...).
Cependant, les AFDs (et les grammaires régulières) sont très souvent inadaptés pour représenter les langages de haut niveau non réguliers. Ces langages sont souvent des langages hors-contexte.
Le moyen le plus adapté pour de tels langages est l'automate à pile permettant d'implanter une analyse descendante (mais il existe aussi d'autres méthodes d'analyse utilisant d'autres algorithmes) et permettant de provoquer des actions après seulement une certaine série de symboles (problème du parenthésage par exemple ainsi que des opérateurs binaires et des expressions arithmétiques).
Ces automates sont déterministes seulement pour des grammaires hors-contexte de type LL(1). Nous n'aborderons pas cela dans le cadre de ce cours mais ce sera étudié en cours de compilation.
Dans l'article fondateur de Shannon (C. E. Shannon, "A Mathematical Theory of Communication", Bell Systems Tech. Jour., XXVII:379-423, 623-656, 1948.), on trouve, comme nous l'avons vu, un modèle très voisin des automates finis, qui est directement issu des chaînes de Markov. Ce modèle est appliqué en particulier à ce que Shannon appelle des approximations du langage naturel. Il s'agit de chaînes de Markov d'ordre croissant réalisant un automate local pour la structure de la langue au niveau lexical (lettre par lettre ou mot par mot). Ainsi, en prenant successivement au hasard des digrammes chevauchant dans un texte en anglais, on obtient l'exemple saisissant :
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT
TEASONARE
FUSO TIZIN ANDY TOBE SEACE CTISBE
dans lequel certains mots existent réellement ('on, are, be... ') et d'autres le mériteraient ('deamy, ilonasive...'). Le résultat obtenu avec des trigrammes au lieu de digrammes est encore plus étonnant :
IN NO IST LAT WHEY CRACTIC FROURE BIRS GROCID PONDENOME OF DEMONSTRURES OF
THE
REPTAGIN IS REGOACTIONA OF CRE
Shannon présente d'autres exemples utilisant des chaînes de Markov au niveau des mots au lieu des lettres. En fait, dès le départ, A. A. Markov a introduit son modèle dans cette perspective et son article, daté de 1913, s'intitule ``Essai d'une recherche statistique sur le texte du roman Eugène Onéguine'' (Bull. Acad. Imper. Sci. St Petersbourg, 7, 1913.).
L'idée d'utiliser des automates pour décrire la langue naturelle est reprise un peu plus tard par Chomsky [Cho56]. En fait, Chomsky n'introduit les automates que pour les écarter assez rapidement au profit du niveau supérieur de ce que l'on nomme aujourd'hui la hiérarchie de Chomsky : automates finis au rez-de-chaussée, automates à pile et grammaires context-free au premier étage, grammaires context-sensitives au second, machines de Turing au dernier. Les arguments employés par Chomsky pour écarter les automates finis comme modèle adéquat des langues naturelles sont fondés sur la présence de structures parenthésées provenant de constructions grammaticales comme les propositions conditionnelles "si S1 alors S2" analogues à celles des langages de programmation et qui permettent, en principe, une imbrication non bornée. Notons que de nombreux modèles autres que les automates ont été proposés pour rendre compte des structures syntaxiques
Le fait que l'anglais ne soit pas un langage rationnel semble aujourd'hui être, à la fois, non prouvable et en balance avec le fait que, de toutes façons, une description complète de la syntaxe de l'anglais (ou du français) est aussi difficile à réaliser sous forme d'automate fini que de grammaire. Les automates finis ayant par contre l'avantage sur les grammaires de se prêter à un grand nombre de manipulations automatisables. Certains, comme Maurice Gross, pensent que ce sont finalement les automates finis qui fournissent l'essentiel de la description (voir M. Gross et D. Perrin, "Electronic Dictionnaries and Automata in Computational Linguistics", Lecture Notes in Computer Science, 377. Springer, 1989.). Du point de vue des automates, la différence essentielle avec les grammaires est le fait que la théorie logique associée aux automates est décidable alors que la plupart des problèmes associés aux grammaires ne le sont pas. Si par exemple on peut assez facilement déterminer si deux automates finis sont équivalents, il n'en est pas de même des grammaires : on peut démontrer que le problème de savoir si deux grammaires sont équivalentes est indécidable.
Nous venons de voir que langage et automates sont utilisés pour générer des programmes et pour comprendre le langage naturel. Cependant, ce ne sont certainement pas les seules utilisations possibles.
Les automates sont aussi souvent utilisés pour modéliser des phénomènes naturels liés au comportement. En particuliers, ils permettent de modéliser des connaissances complexes ainsi que des règles de comportement dépendant d'événement <<extérieurs>>. Pour cela, il est possible d'utiliser des réseaux de Pétri. En particulier, les modèles de comportement en animation se basent sur des graphes d'événements.
Dans certains cas, le comportement est aussi lié à des paramètres stochastiques. Aussi, lorsque l'automate n'est pas déterministe, il est parfois associé aux transitions sur un même symbole (ou événement) un paramètre probabiliste : ce sont les automates stockastiques ou chaînes de Markov. Ces automates permettent, en particulier, de modéliser la gestion de files d'attentes...
Les automates sont aussi utilisés en modélisation et conception de systèmes. Une modélisation OMT ou UML consiste non seulement en une description des objets mis en jeu mais aussi leurs relations vis-à-vis des divers évènements.
Toujours lié au comportement de systèmes, on trouve des applications des automates pour la gestion du dialogue Homme-Machine et pour la conception de jeux.
jeudi, 27/05/04 15:17