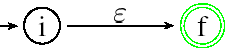
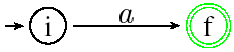
Du fait de l'équivalence entre langages reconaissables et langages rationnels, des méthodes permettant de passer d'une expression rationnelle à un AFN ont été mises au point.
Remarque : un intérêt de cette conversion est la possibilité de mettre en place des traitements de validation de suites de symboles ou d'évènements dans des langages ne gérant pas les expressions rationnelles ou lorsque les traitements associés ne sont pas facilement descriptibles ou pas très performants dans ces langages.
Il existe de nombreuses stratégies pour construire de façon automatique un automate fini à partir d'une expression rationnelle [Watson93a] (cette référence présente de manière formelle différents algorithmes dont celui de Thompson). L'algorithme présenté ici est l'algorithme de construction de Thompson [Thompson68]. Plusieurs variantes sont possibles. Celle présentée ici est simple et surtout facile à implanter (ce qui n'est pas le cas de toutes les méthodes).
L'algorithme est dirigé par la syntaxe, c'est-à-dire qu'il utilise la structure syntaxique de l'expression rationnelle pour guider le processus de construction. Il est récursif sur l'arbre syntaxique de l'expression rationnelle. A partir d'une expression r sur un alphabet A, on cherche à construire un AFN T(r) qui reconnaît L(r) (le langage reconnu par r).
Si l'expression est réduite à un symbole s alors on construit l'automate :
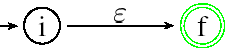
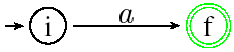
Si l'expression n'est pas un symbole, il faut alors la décomposer selon l'opérateur utilisé puis construire les automates T(r1)=T1={A, Q1, I1={i1}, F1={f1}, μ1} et T(r2)=T2={A, Q2, I2={i2}, F2={f2}, μ2} associés aux opérandes r1 et r2. Enfin, selon le type d'expression :
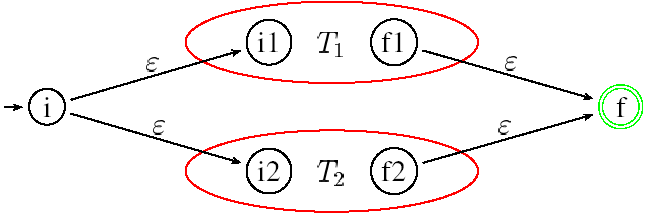
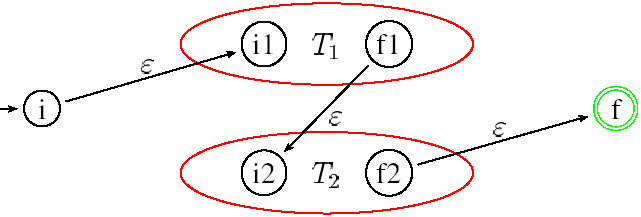
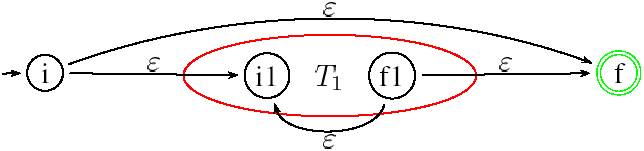
Chaque fois que l'on construit un nouvel état, on lui donne un nom distinct pour qu'il n'y ait pas deux états de même nom. Même si un symbole apparaît plusieurs fois dans l'expression rationnelle, on crée pour chaque symbole un AFN séparé avec ses propres états. Chaque étape de la construction produit un AFN qui reconnaît le langage correct.
L'AFN ainsi produit possède les propriétés suivantes :
Appliquons de cet algorithme sur l'expression régulière (a2 | b*a+)*. Tout d'abord, il faut construire l'arbre syntaxique associé à cette expression (attention, plusieurs arbres sont souvent possibles) :
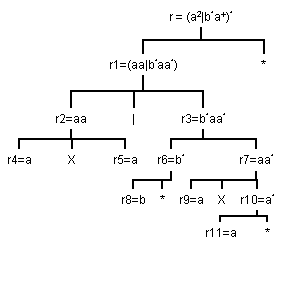
Ensuite, il suffit d'appliquer les règles de Thompson en partant des feuilles. Donc, il faut d'abord construire r4, r5, r8, r9 et r11.
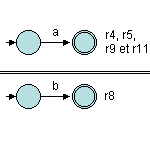
Remarque : il n'est pas toujours nécessaire d'étiqueter (numéroter) les états. Dans ce type d'algorithme, il n'est pas utile de les repérer (pas nécessaire de les identifier).
Ensuite, il faut construire r2, r6 et r10 :
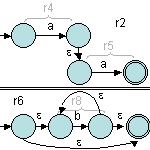
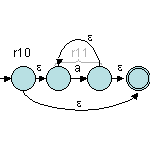
Puis, on construit r7 :
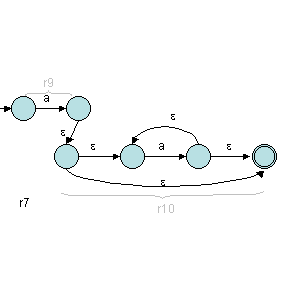
Puis, c'est le tour de r3 :
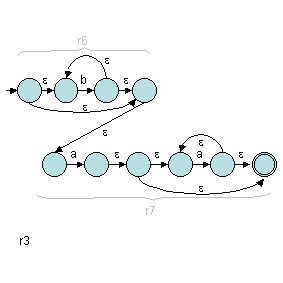
Ensuite, c'est r1 :
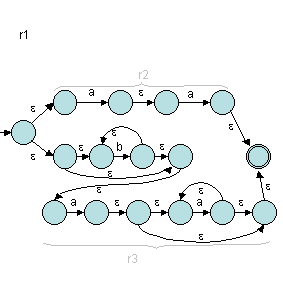
Pour terminer, r permet de construire l'automate suivant :
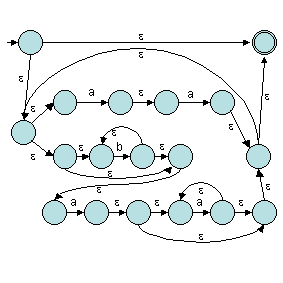
Ouf !
Sur l'expression (a|b)*abb, Thompson permet d'obtenir l'automate suivant :
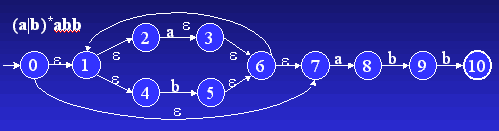
Ici, le produit est effectué par fusion de l'état final du premier avec l'état initial du second.
Remarque : il est possible de construire directement un AFD à partir d'une expression régulière dite "étendue", c'est-à-dire à laquelle on ajoute en fin le caractère #. Nous n'aborderons pas cette méthode ici (voir [ASU91], pp.159-165).
Bien évidemment, l'algorithme de Thompson n'est pas le seul possible. Il en existe de nombreux dont celui de Glushkov. Cette algorithme est intéressant, car il construit un automate ε-libre et homogène.
Le principe de cette méthode est le suivant : si tous les symboles de l'expression sont différents alors il est possible d'associer un état à chaque symbole et une transition est présente entre deux états si les deux symboles associés se suivent dans un mot du langage.
Plus précisément, cette méthode se divise en 4 étapes :
Pour l'étape 1, si un symbole représente une classe de symboles alors on peut se contenter de ce symbole mais en phase 4 il faudra créer autant de transitions qu'il y a de symboles de l'alphabet dans la classe.
Il faut noter aussi que l'expression ne doit pas contenir ε afin de ne pas générer un automate avec des ε-transitions.
Reprenons notre exemple habituel, l'expression (a2| b*a+)*. On passe alors par les étapes suivantes :
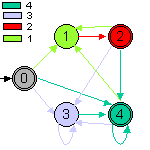 (pour
alléger l'automate, une couleur est associée à chaque
numéro)
(pour
alléger l'automate, une couleur est associée à chaque
numéro) 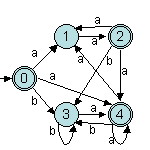
De cet exemple, on déduit que l'automate produit à de grandes chances de ne pas être déterministe.
Du théorème de Kleene et de ses conséquences, nous en déduisons facilement une méthode manuelle pour construire un AFN à partir d'une expression rationnelle. Il suffit de décomposer l'expression comme une suite d'opérations (produit, union et étoile) sur des langages typiques ou réduits à un mot voire à un symbole. Puis on construit les automates finis correspondant à ces langages "élémentaires" ( Cf. la démonstration du lemme du langage réduit à un mot). On applique ensuite les opérateurs sur ces automates (Cf. démonstrations des théorèmes du produit cartésien, de la mise à l'étoile et de l'union).
Remarque : la décomposition peut être arrêtée dès que l'on voit apparaître une expression dont l'automate est "classique" (a*, a+, a?, a|b...).
Par exemple, étudions le langage décrit par (a2| b*a+)*.
Les automates reconnaissant r1=a2, r2=b* et r3=a+ sont faciles à obtenir :
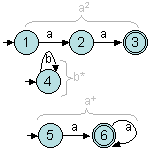
Ensuite, on construit l'automate produit reconnaissant r4=r2r3 :
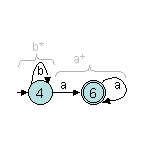
Ensuite, nous obtenons r0 par l'union de r1 avec r4 :
a |
b |
|
1,4∈ I |
2,6 |
0,4 |
2,6 ∈ F |
3,6 |
0,0 |
0,4 |
0,6 |
0,4 |
3,6 ∈ F |
0,6 |
0,0 |
0,6 ∈ F |
0,6 |
0,0 |
D'où : 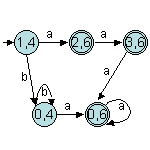
En minimisant (ou en réfléchissant dès le départ car a2 ⊂ b*a+ !) on obtient r0=r4 !
Enfin, r = r4* donne l'automate homogène suivant :
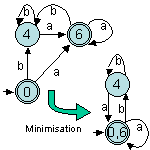
Nous venons de présenter des méthodes permettant de passer d'une expression rationnelle décrivant un langage à un automate fini (déterministe minimal) le reconnaissant. Cependant, il est souvent plus facile de définir un langage à l'aide d'un ensemble d'expressions plutôt qu'avec une seule et unique expression. Pour cela, il est possible de donner un ensemble de définitions rationnelles. Le langage décrit est alors l'union des langages définis par chacune des définitions.
Par exemple, supposons un langage L composé d'identificateurs et d'entiers, il y aura alors les deux définitions rationnelles (elles-mêmes basées sur deux classes de symboles) suivantes :
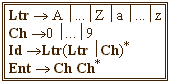
Nous allons maintenant présenter une méthode pour regrouper les différents automates associés à chacune des définitions.
Soit une suite de définitions rationnelles de la forme :
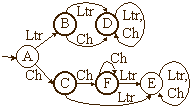
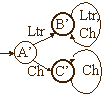
La génération pour cet ensemble d'expressions rationnelles passera par les étapes suivantes (en figures l'application sur L) :
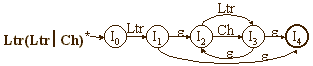
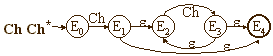
Exercices et tests :
Exercice 3.1. Donner les automates finis reconnaissant les langages définis par les expressions rationnelles suivantes sur {a,b,c} selon les trois méthodes vues dans cette section (méthode intuitive, de Thompson et de Glushkov) :
Exercice 3.2. Donner l'automate fini optimal reconnaissant le langage défini par l'expression rationnelle suivante sur {a,b} : (ab*)|(ab)*
mardi, 25/11/03 17:02