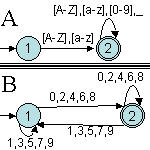7. Propriétés
des AFNs
7.1. Dimension d'un automate
Outre le fait qu'un automate soit ou non déterministe,
il est possible de mettre en évidence d'autres caractéristiques.
La dimension d'un automate fini correspond simplement au nombre d'états
qu'il possède. Cette dimension peut être minimale lorsqu'il n'est
plus possible de trouver un automate équivalent de dimension strictement
inférieure.
| 
Dimension d'un AFN
AFN minimal
|
La
dimension d'un AFN T=(A, Q, I, F, μ), notée
|T| est définie par :
|T | = |Q|. Autrement dit, la dimension d'un automate est le nombre d'états
de cet automate.
Un
automate de dimension minimale est un automate T tel
que ∀ T', T' ≡ T alors |T'| ≥ |T|. |
7.2. Propriétés liées aux caractéristiques des
états
Un automate fini complet est un automate pour lequel, pour toute configuration,
il existe une transition vers un état de cet automate. La fonction d'appartenance
est totalement définie (pour tout couple (symbole courant, état
courant)).
| 
AFN complet
|
Un
AFN complet T=(A, Q, I, F, μ) est un AFN vérifiant
:
Complet(T) ≡ (μ(a,q) ≠ 0, ∀ q ∈ Q, ∀ a
∈ A) avec 0 l'état d'erreur. |
Remarque : si Complet(T) alors {∪ LG(q), ∀ q ∈ Q} = A*.
Pour rendre un automate complet (la complétion), il suffit d'ajouter
un état puit "p" et d'y diriger toutes les transitions manquantes.
Si T={A, Q, I, F, μ} alors Completion(T) = {A, Q ∪ {p}, I, F, μ'}
avec μ' = μ ∪ {(q,a,p) : ∀ q' ∈ Q, (q,a,q') ∉ μ}
∪ {(p,a,p) : ∀ a}. Le langage n'est pas modifié car on ajoute
un état qui n'est pas final et des transitions initialement absentes
vers cet état.
Un automate fini est utile si tout état de cet automate possède
un langage gauche et un langage droit, c'est-à-dire si tout état
de l'automate peut être utilisé pour reconnaître au moins
un mot du langage.
| 
AFN utile
AFN émondé
|
Soit
un AFN T=(A, Q, I, F, μ) :
- UtileI est défini
par : UtileI(T) ≡ utileI(q), ∀ q
∈ Q ;
- UtileF est défini
par :UtileF(T) ≡ utileF(q), ∀ q ∈
Q ;
Un
AFN émondé (ou utile) est un AFN dont tous
les états sont utiles. Donc : Emondé(T) ≡ UtileI(T)
∧ UtileF(T) ≡ utile(q), ∀ q ∈ Q. |
Il est possible d'en déduire une relation entre langage reconnaissable
et automate émondé.
| 
Théorème
de l'émondage
|
Pour tout langage
reconnaissable L sur un alphabet A (ie L ∈ Rec(A*)) il existe un
automate émondé qui le reconnait. |
Démonstration :
La démonstration se fait par construction de l'automate émondé
à partir d'un AFN T=(A, Q, I, F, μ) qui reconnaît le langage (algorithme
de l'émondage) :
- Détermination de l'ensemble w des états accessibles
- Soit wi l'ensemble des états accessibles à
l'instant i.
Au départ, les seuls états accessibles sont les états
initiaux, donc w0 = I
- Tout état q est accessible s'il existe une transition μ(a,p)=q
avec p lui-même accessible. Donc,
wi+1 = wi ∪ {q | q ∈ Q, ∃ p ∈
wi et ∃ a ∈ A tels que μ(a,p)=q}
- C'est terminé quand wi+1 = wi donc
w = wi
- Détermination de l'ensemble z des états co-accessibles
- Soit zi l'ensemble des états co-accessibles à
l'instant i. Au départ, seuls les états finaux sont
co-accessibles, donc z0 = F
- Tout état q est co-accessible s'il existe une transition
μ(a,q)=p avec p lui-même co-accessible. Donc,
zi+1 = zi ∪ {q | q ∈ Q, ∃ p ∈
zi et ∃ a ∈ A tels que μ(a,q)=p}
- C'est terminé quand zi+1 = zi donc
z = zi
- Construction de l'automate émondé T' :
T'=(A, Q' = w ∩ z, I' = I ∩ w ∩ z, F' = F ∩ w ∩ z,
μ') avec μ'= {(q,a,q') | (q,a,q') ∈ μ, q, q' ∈ Q'}
L'automate obtenu est équivalent à l'automate d'origine.
Sur un exemple, cela donne les étapes suivantes :
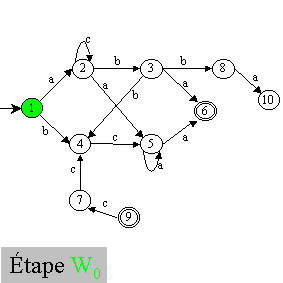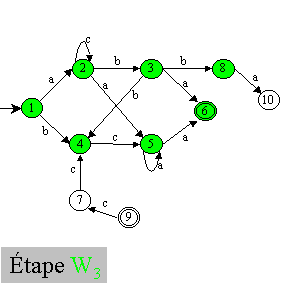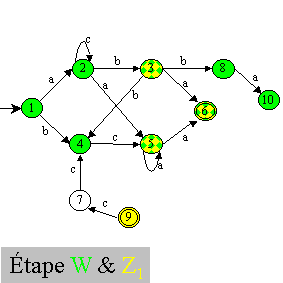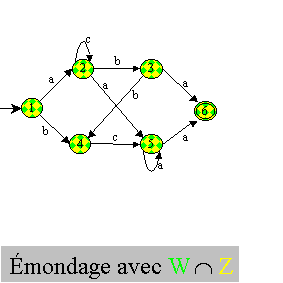
Remarque : il est possible d'améliorer un peu cet algorithme en initialisant
z0 non pas à F mais à F ∩ w. De plus, on ne met
dans z que les états étant déjà dans w. Du coup,
au final, Q'=z.
7.3. Propriétés sur la structure de l'automate
Un autre ensemble de propriétés concerne le nombre des états
initiaux et finaux ainsi que les transitions qui les concernent. Nous avons
alors les définitions suivantes :
| 
AFN unitaire
AFN standard
AFN normalisé
AFN homogène
|
Un
AFN T=(A, Q, I, F, μ) est dit unitaire s'il ne possède
qu'un seul état initial, c'est-à-dire que I={i} avec i ∈
Q.
Un
AFN T=(A, Q, I, F, μ) est dit standard s'il est unitaire
(I={i}) et si {μ(a,q)=i | x ∈ A, q ∈ Q, I={i}} = ∅.
Autrement dit, aucune transition arrive sur le seul état initial.
Un AFN
T=(A, Q, I, F, μ) est dit normalisé s'il est
standard et si F={f] avec f ∈
F et {μ(a,f)=q | x ∈ A, q ∈ Q, I={i}} = ∅. Autrement
dit, s'il est standard et ne possède qu'un seul état final
et qu'aucune transition n'a pour origine cet état final.
Un AFN
T=(A, Q, I, F, μ) est dit homogène si toutes
les transitions qui arrivent sur un état sont sur le même
symbole de l'alphabet. |
Les propriétés "standard" et "normalisé"
ne sont pas limitatives en ce qui concerne l'automate reconnu. En effet, tout
langage reconnaissable peut l'être par un automate standard et même
normalisé.
| 
Théorème
de l'automate standard
|
Pour tout langage
reconnaissable L sur un alphabet A (ie L ∈ Rec(A*)) il existe un
automate standard qui le reconnait. |
Démonstration :
La démonstration se fait par construction de l'automate standard à
partir d'un AFN T=(A, Q, I, F, μ) qui reconnaît le langage (algorithme
de la standardisation) :
- Soit T' l'automate standard équivalent à T,
T'={A, Q ∪ {d}, {d}, F', μ'}
- d ∉ Q
- F' = F ∪ {d} si I ∩ F ≠ ∅
F' = F sinon
- μ' = μ ∪ {(d,a,q) | (i,a,q) ∈ μ, i ∈ I}
Montrons que l'automate standard T' ainsi obtenu reconnaît bien le même
langage que T. Autrement dit, montrons que L(T)
= L(Standard(T)) = L(T').
La figure suivante montre un exemple de standardisation d'un automate fini.
L'état et les transitions ajoutés par l'algorithme sont en vert
"fluo". Ce qui est en rouge disparaît par l'algorithme.
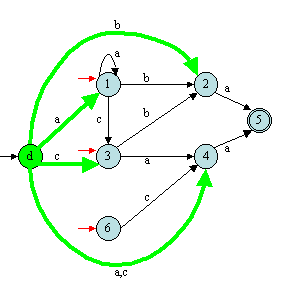
Remarque : dans cet exemple, après la standardisation, l'état
6 n'est plus un état final. Comme aucune transition n'arrive sur celui-ci,
il devient alors inaccessible. Aussi, il est préférable de lancer
un émondage après une standardisation pour éliminer ces
états inutiles.
| 
Théorème de l'automate normalisé
|
Pour
tout langage reconnaissable L sur un alphabet A (ie L ∈ Rec(A*))
il existe un automate normalisé qui le reconnaît. |
Démonstration :
La démonstration se fait par construction de l'automate normalisé
à partir d'un AFN T=(A, Q, I, F, μ) qui reconnaît le langage : similaire
à la démonstration du théorème
de l'automate standard.
7.4. Cas des automates avec des ε-transitions
Parmi les transitions possibles dans un AFN, il en existe une particulièrement
spécifique appelée l'ε-transition (epsilon-transition).
De telles transitions sont caractéristiques des automates non déterministes.
| 
ε-transition
|
Une
ε-transition est une transition qui n'utilise
aucune entrée. C'est une transition <<spontanée>>,
c'est-à-dire que l'automate <<décide>> simplement
de changer d'état sans lire de symbole. |
La figure suivante montre un automate comportant des ε-transitions
(en vert). Il reconnait le langage sur l'alphabet {a,b} dont les mots terminent
par le suffixe "abb".
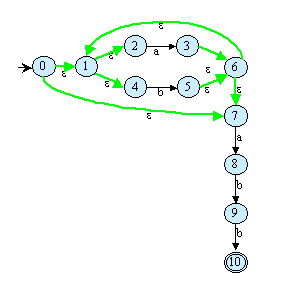
Ces transitions très particulières sont principalement introduites
lors de la construction automatique d'un automate à partir d'une expression
rationnelle (vue plus loin). Cependant,
de part leur nature, elles sont à éviter. Nous
verrons comment les supprimer en présentant la déterminisation
d'un AFN. L'AFN sans ε-transition est appelé ε-libre.
| 
AFN ε-libre
|
Un
AFN T=(A, Q, I, F, μ) est dit ε-libre s'il
ne possède pas de ε-transition,
c'est-à-dire si : μ(ε,a)=0, ∀ q ∈ Q. |
Remarque : Même si un AFN T=(A, Q, I, F, μ) est ε-libre, il
est possible que ε ∈ L(T) quand I ∈ F.
7.5. Automates déterministes (AFD)
Lorsqu'il n'existe au plus qu'une seule action possible au maximum pour une
configuration donnée, l'automate fini est alors dit déterministe.
| 
Automate fini déterministe
AFD
|
Un
AFN T=(A, Q, I, F, μ) est dit déterministe
(AFD) si :
- il est ε-libre
- il est unitaire
- si ∀ q ∈ Q, ∀
a ∈ A : |μ(a,q)| ≤ 1.
Autrement dit, si μ(a,q)=q1 et μ(a,q)=q2
si et seulement si q1=q2.
|
Notation : L'expression |μ(a,q)| avec q ∈ Q, a ∈ A indique le
nombre de transitions existant dans l'automate sur la configuration (aw,q),
w ∈ A*.
Les AFDs sont intéressants car, lors d'une analyse, ils ne posent pas
de problèmes de choix : pour un état et un symbole, il n'existe
au plus qu'une seule transition possible. L'acceptation avec de tels automates
est alors plus facile et souvent plus performante. Nous proposerons plus loin
un algorithme pour rendre déterministe un automate
fini quelconque.
Remarque : Parfois, on trouve la notion d'automate faiblement déterministe.
Un AFN T=(A, Q, I, F, μ) est dit faiblement déterministe (AFd) si
: ∀ q0 ∈ Q, ∀ q1 ∈ Q, q0
≠ q1, LG(q0) ∩ LD(q1) = ∅. On
peut montrer que si T est un AFD alors T est un AFd.
7.6. AFD minimal
Un automate fini déterministe de dimension minimale est un cas particulier
d'AFD pour lequel il n'existe pas d'AFD équivalent possédant moins
d'états. Par contre, il est possible qu'il y en ait avec autant d'états
(l'AFD de dimension minimale n'est pas unique).
Par contre, un automate fini minimal est unique. Pour définir un automate
minimal, il est possible de s'appuyer sur les notions d'états indistinguables
et d'automates réduits.
Il est possible de comparer le rôle de deux états dans un automate
par rapport aux mots reconnus : la notion d'états distinguables ou indistinguables.
| 
Etats distinguables
Etats k-indistinguables
|
Soit
un AFD T=(A, Q, I, F, μ), on dit que la chaîne d'entrée
w ∈ A* distingue l'état e de l'état f (e ≠ f) dans
T si :
- partant de l'état
e et le faisant fonctionner avec w, on termine dans un état d'acceptation
;
- partant de l'état f
et le faisant fonctionner avec w, on termine dans un état de
non-acceptation (ou vice versa).
Les états e et f sont
alors dits distinguables. Autrement dit, w distingue
e et f si ∃ q1, q2 ∈ Q, (w, e) —*/T→
(ε, q1) et (w, f) —*/T→ (ε, q2)
avec exactement 1 des états q1 ou q2 ∈
F.
Deux
états e et f d'un AFD T sont k-indistinguables,
noté e ≡k≡ f si : ∀ w ∈ A*, |w| ≤ k
w ne distingue pas e et f.
Deux
états e et f d'un AFD T sont indistinguables,
si ∀ k ≥ 0, e ≡k≡ f. |
Remarque : e et f sont distinguables s'ils vérifient la condition suivante
: (w ∈ LD(e) et w ∉ LD(f)) ou (w ∈ LD(f) et w ∉ LD(e))
Un automate réduit est un automate qui ne possède pas de couples
d'états indistinguables.
| 
Automate réduit
|
Un
AFD T=(A, Q, I, F, μ) est dit réduit si tous
les états de Q sont accessibles
et si tous les d'états de Q pris deux à deux sont distinguables.
|
Un automate minimal est alors un automate réduit dont on ne peut trouver
un automate équivalent avec un nombre d'états strictement inférieur
au sien (de dimension minimale). Cet automate est unique à la numérotation
des états près.
| 
Automate minimal
|
Un
AFD T=(A, Q, I, F, μ) est dit minimal s'il est réduit
et si : Min(T) ≡ ∀ T' ∈ AFD, L(T) = L(T') : |T| ≤
|T'|.
Un AFD T=(A, Q, I, F, μ) est
dit minimal complet si : MinC(T) ≡ ∀
T' ∈ AFD, Complet(T'), L(T) =
L(T') : |T| ≤ |T'|. |
Nous verrons plus loin un algorithme pour minimiser
un automate fini.
7.7. Quelques langages et leurs automates
Beaucoup d'opérations sur les langages reconnaissables ont un algorithme
associé sur les automates qui les reconnaissent. Nous allons en étudier
trois ici, d'autres viendrons dans une prochaine section.
| 
Théorème
des facteurs
|
Pour tout langage
reconnaissable L sur un alphabet A (ie L ∈ Rec(A*)), Pref(L) (le
langage des préfixes des mots L), Suff(L) (le langage des suffixes
des mots de L) et Fact(L) (le langage des facteurs dans L) sont aussi
reconnaissables. |
Démonstration :
La démonstration se fait par construction des automates à partir
d'un AFN T=(A, Q, I, F, μ) qui reconnait le langage L :
- TPref = {A, Q, I, Q, μ} si utileF(T) (ie, tous
les états sont co-accessibles)
- TSuff = {A, Q, Q, F, μ} si utileI(T) (ie, tous
les états sont accessibles)
- TFact = {A, Q, Q, Q, μ} si émondé(T) (ie,
tous les états sont accessibles et co-accessibles)
Exercices et tests :
Exercice 7.1. Montrer pourquoi
un automate fini normalisé n'est jamais complet.


Exercice 7.2. Donner les propriétés
(la minimalité n'est pas demandée) des automates suivants (images
issues de JFLAP ; avec ce logiciel les ε-transitions
sont notée λ) :
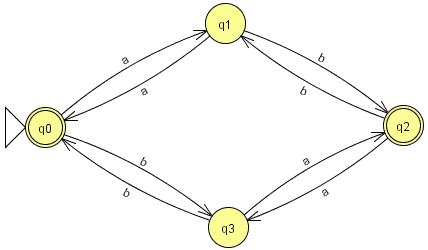
sur l'alphabet {a,b}
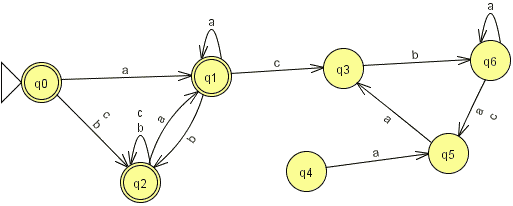
sur l'alphabet {a,b,c,d}
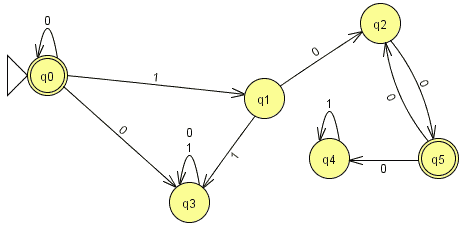
sur l'alphabet {0,1,2,3,4,5,6,7,8,9}
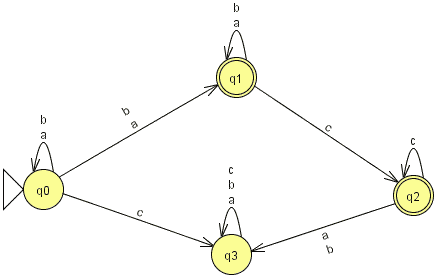
sur l'alphabet {a,b,c,d}
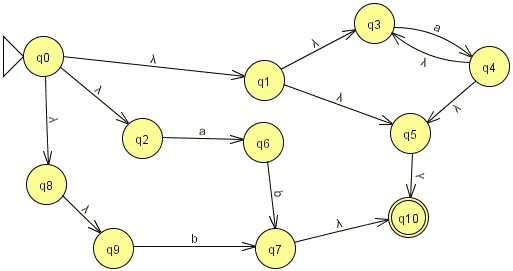
sur l'alphabet {a,b}

Exercice 7.3. Les automates
suivants sont-ils déterministes :
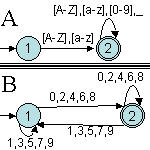
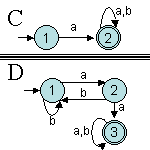
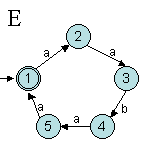
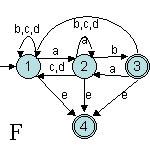

mercredi, 17/12/03 12:33
![]()