![]()
Théorème de l'AFD minimal réduit
L'automate T' obtenu par cet algorithme est minimal.
Après avoir introduit les automates finis non déterministes (AFN) et déterministes (AFD) et présenté un algorithme permettant de passer d'un AFN à un AFD, nous allons étudier une méthode permettant de simplifier, minimiser, un AFD.
Certains AFDs possèdent un nombre d'états et de transitions important. États et transitions ne sont pas toujours indispensables. Typiquement, cette situation a lieu lorsque l'automate est construit à l'aide d'algorithmes automatiques comme dans le cas de la construction automatique d'un AFN et de la transformation d'un AFN en AFD. Afin d'améliorer la reconnaissance des chaînes et d'optimiser la place mémoire utilisée, il est intéressant d'essayer de minimiser un AFD. Une première approche de cette minimisation peut consister à étudier les caractéristiques des états et de supprimer ceux qui sont inutiles. Cependant, il est possible d'aller plus loin en garantissant que l'AFD obtenu est un AFD minimal. Ceci est l'objectif de la méthode que l'on présente ici.
Il existe de nombreuses stratégies pour minimiser un AFD [Wat93b]. Dans cette référence, on trouvera aussi la formalisation et la caractérisation des classes d'équivalence. L'algorithme de Moore présenté ici est un algorithme, issu de [ASU91], basé sur les classes d'équivalence d'états.
L'algorithme de minimisation du nombre d'états d'un AFD fonctionne en déterminant tous les groupes d'états qui peuvent être distingués par une chaîne d'entrée. Chaque groupe d'états indistinguables est alors fusionné en un état unique. L'algorithme travaille en mémorisant et en raffinant une partition de l'ensemble des états. Chaque groupe d'états à l'intérieur de la partition correspond aux états qui n'ont pas encore été distingués les uns des autres. Toute paire d'états extraits de différents groupes a été prouvée "distinguable" par une chaîne.
Initialement, la partition consiste à former deux groupes : les états d'acceptation et les autres. L'étape fondamentale prend un groupe d'états et un symbole puis étudie les transitions de ces états sur ce symbole. Si ces transitions conduisent à des états qui tombent dans au moins deux groupes différents de la partition courante, alors on doit diviser ce groupe. La division est effectuée avec pour objectif que les transitions depuis chaque sous-groupe soient confinées à un seul groupe de la partition courante. Ce processus de division est répété jusqu'à ce qu'aucun groupe n'ait plus besoin d'être divisé.
Les états du nouvel automate sont donnés par un représentant de chaque groupe. Les états finaux sont les représentants des groupes possédant un état final de l'AFD de départ. L'état de départ est le représentant du groupe possédant l'état de départ de l'AFD initial. Les transitions sont construites avec les transitions de chaque état représentant de groupe vers un état représentant d'un autre groupe si cet état engendre une transition vers un élément du groupe.
Sur les états créés, il faut supprimer les états stériles et les états non-accessibles depuis l'état initial.
|
|
L'automate T' obtenu par cet algorithme est minimal. |
Remarque : cette méthode de minimisation (comme pour la méthode de déterminisation) est applicable par la manipulation d'une table de transitions. La première ligne donne pour chacun des états son appartenance à un des deux ensembles de départ. Ensuite, pour chaque état et chaque symbole on détermine vers quel ensemble nous mène la transition correspondante. Une fois tous les couples étudiés, on divise les ensembles de départ en ensembles dont les états se comportent de la même manière. On recommence jusqu'à ce qu'il n'y ait plus de division d'ensemble. L'exemple suivant illustre cette manière de faire.
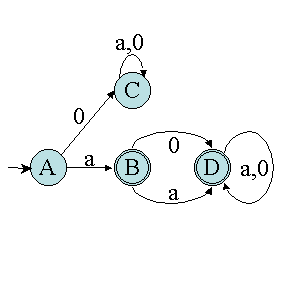
Si on applique cet algorithme à l'automate déterministe de l'exemple 2 de la section précédente (automate ci-dessus), la phase d'initialisation permet d'obtenir :
A |
B |
C |
D |
|
| ε (initialisation) | I |
II |
I |
II |
| a | ||||
| 0 | ||||
| Bilan 1 |
En effet, A et C ne sont pas des état finaux. Ils sont donc dans le même ensemble (noté I). De même, B et C sont finaux. Ils sont donc dans le même ensemble (noté II).
Ensuite, pour chaque couple (état, symbole), on regarde vers quel ensemble nous mène la transition de l'automate (si elle existe, sinon on ne met rien).
A |
B |
C |
D |
|
| ε (initialisation) | I |
II |
I |
II |
| a | II |
II |
I |
II |
| 0 | I |
II |
I |
II |
| Bilan 1 |
Puis on effectue la séparation des ensembles. Deux états sont dans un même ensemble s'ils étaient déjà dans le même ensemble et si les transitions mènent dans les mêmes ensembles. Dans cet exemple, B et D se comportent exactement de la même manière, donc ils restent ensemble. Par contre, A et C qui faisaient partie du même ensemble se comportent différemment sur le symbole "a". Par conséquent, l'ensemble noté I se divise en deux. Nous obtenons donc :
A |
B |
C |
D |
|
| ε (initialisation) | I |
II |
I |
II |
| a | II |
II |
I |
II |
| 0 | I |
II |
I |
II |
| Bilan 1 | I |
II |
III |
II |
La situation courante (la ligne Bilan 1) est différente que la situation de départ. Donc il faut recommencer !
A |
B |
C |
D |
|
| ε (initialisation) | I |
II |
I |
II |
| a | II |
II |
I |
II |
| 0 | I |
II |
I |
II |
| Bilan 1 | I |
II |
III |
II |
| a | II |
II |
III |
II |
| 0 | III |
II |
III |
II |
| Bilan 2 | I |
II |
III |
II |
La ligne "Bilan 2" est identique à la ligne "Bilan 1". Par conséquent, dans chacun des ensembles restants, les états ne sont pas distinguables (ils se comportent exactement de la même manière et sont donc "redondants").
Nous pouvons donc construire le nouvel automate en associant un état à chaque ensemble. Les transitions sont indiquées par le tableau. L'état initial est celui contenant l'état initial de l'automate de départ : ici I contient l'état A, état initial. Les états finaux sont les états dont l'ensemble correspondant contient au moins un état final : ici, II contient B et D qui sont finaux.
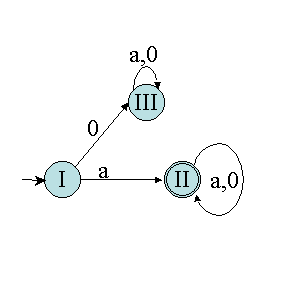
Cependant, l'algorithme n'est pas encore terminé ! Pour l'instant, nous avons "fusionné" les états indistinguables. Il faut maintenant supprimer tous les états inutiles restant. Dans notre exemple, l'état III est un état stérile, donc inutile. Il faut donc le supprimer. D'où l'automate déterministe minimal de la figure suivante.
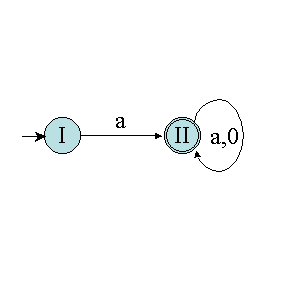
Considérons maintenant l'exemple A de la section précédente :
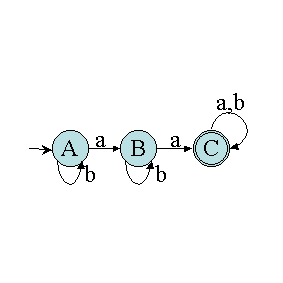
Appliquons la même méthode de minimisation :
A |
B |
C |
|
| ε (initialisation) | I |
I |
II |
| a | I |
II |
II |
| b | I |
I |
II |
| Bilan 1 | I |
II |
III |
| a | |||
| b | |||
| Bilan 2 |
A ce stade, le bilan 1 est différent de l'état initial. Cependant, il y a autant d'ensembles que d'états (ou seulement un état par ensemble). Il ne peut donc pas y avoir d'autre division d'ensemble. Par conséquent, nous pouvons arrêter là le traitement. Notons que nous obtenons exactement le même automate que celui de départ (à la numérotation près). Par conséquent, nous avions un automate déjà minimal !
Pour des automates complexes, cet algorithme peut s'avérer coûteux. Aussi, il est préférable d'effectuer un pré-traitement permettant de réduire simplement le nombre d'états de l'automate.
Une première idée est d'appliquer l'algorithme d'émondage pour supprimer les états de l'AFD qui sont inutiles.
Une seconde idée consiste à supprimer les états qui ont les mêmes transitions pour n'en garder qu'une seule. Par exemple, prenons la table de transition suivante :
μ |
a |
b |
v |
x |
|
x |
z |
t |
u |
y |
|
y |
z |
t |
t |
x |
y |
z |
Les transitions partant de x et de y sont les mêmes. Par conséquent, x et y ne sont pas distinguables. Donc, il est possible d'en supprimer un : par exemple y. Toutes les transitions menant à y sont alors dirigées vers x. Nous obtenons alors la table suivante :
μ |
a |
b |
v |
x |
|
x |
z |
t |
u |
x |
|
t |
x |
x |
z |
Pour vérifier si un automate déterministe est minimal, il suffit d'appliquer l'algorithme de minimisation. Ensuite, si les deux automates sont identiques (à la numérotation des états près) alors l'automate d'origine est minimal.
Il existe aussi une heuristique permettant de vérifier la "minimalité" d'un automate en se basant sur le langage qu'il reconnaît. Si ce langage est de la forme u* alors le nombre d'état est |u|. Dans le cas contraire, le nombre d'état sera |x| où x est le plus petit mot du langage en dehors d'ε.
Deux automates finis sont équivalents s'ils reconnaissent le même langage. Cependant, il n'est pas toujours facile et même possible de se baser sur le langage pour les comparer (surtout s'il est infini !). Par contre, pour un langage donné, il n'existe qu'un unique AFD minimal (à la numérotation des états près). C'est pour cela que l'automate déterministe minimal est parfois appelé "Automate Canonique".
Par conséquent, pour comparer deux automates, il suffit, pour chacun d'eux, de calculer l'automate déterministe minimal équivalent et de comparer ces deux automates.
Pour comparer deux automates déterministe minimaux, il suffit de parcourir en parallèle les deux automates et de renuméroter les états rencontrés en fur et à mesure. A la fin du parcours, les deux tables de transitions doivent être identiques.
Remarque : il existe certainement d'autres techniques issues de la théorie des graphes à propos de la comparaison de graphes.
Exercices et tests :
Exercice 9.1. Soit l'automate déterministe suivant sur l'alphabet {a,b,c} (image issue de JFLAP) :
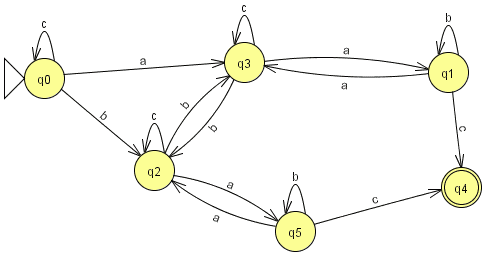
Donner l'automate déterministe minimal équivalent par la méthode de Moore (donner le détail de la méthode).
Exercice 9.2. Soit l'automate suivant sur l'alphabet {a,b,c} (image issue de JFLAP) :
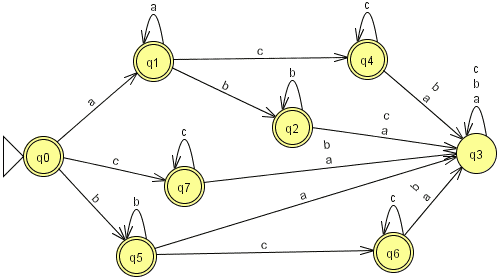
Donner l'automate déterministe minimal équivalent par la méthode
de Moore (donner le détail de la méthode).
![]()
Exercice 9.3. Soit l'automate suivant sur l'alphabet {a,b} (image issue de JFLAP) :
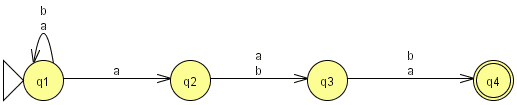
Donner l'automate déterministe minimal équivalent par la méthode
de construction des sous-ensembles et la méthode de Moore (donner le
détail des méthodes).
![]()
Exercice 9.4. Soit l'automate suivant sur l'alphabet {a,b,c} :
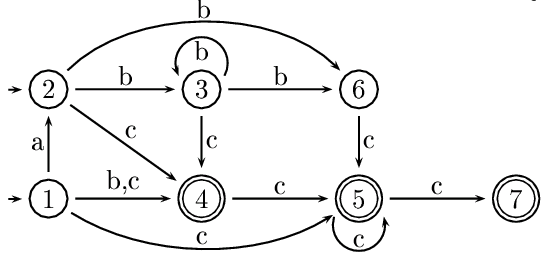
Donner l'automate déterministe minimal équivalent par la méthode
de construction des sous-ensembles et la méthode de Moore (donner le
détail des méthodes).
![]()
Exercice 9.5. Soit les automates suivant sur l'alphabet {a,b} (images issues de JFLAP):
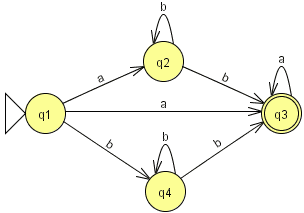
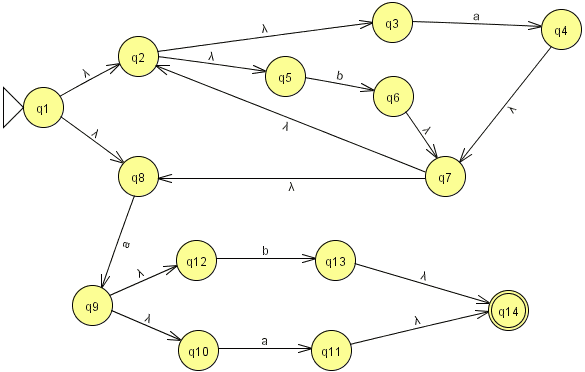
Donner les automates déterministes minimaux équivalents respectifs par la méthode de construction des sous-ensembles et la méthode de Moore (donner le détail des méthodes).
mercredi, 17/12/03 12:41